题目内容
【题目】某农场预算用5600元购买单价为50元（每吨）的钾肥和20元（每吨）的氮肥，希望使两种肥料的总数量（吨）尽可能的多，但氮肥数不少于钾肥数，且不多于钾肥数的1.5倍
(Ⅰ)设买钾肥
吨，买氮肥
吨，按题意列出约束条件、画出可行域，并求钾肥、氮肥各买多少才行？
(Ⅱ)已知
，
是坐标原点， 
在(Ⅰ)中的可行域内，求
的取值范围.
【答案】(Ⅰ) 购买钾肥70吨，氮肥105吨时，两种肥料的总数量最大为175吨(Ⅱ)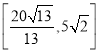 
【解析】
试题分析：(Ⅰ)首先由已知条件中的限定条件可得到关于x,y的不等式，从而确定线性约束条件，进而由不等式得到可行域，通过对目标函数
的变形，将z赋予特定的几何含义：直线的截距，从而求得z取最值时x,y的取值；(Ⅱ) 将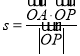
代入点的坐标转化为
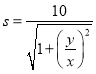，借助于斜率求解s的取值范围
试题解析：(Ⅰ)设肥料总数为
，
由题意得约束条件
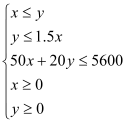，即
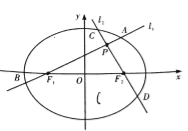
画出可行域（如图）
目标函数：，即
，
表示斜率为
，
轴上截距为
的平行直线系.
当直线过点N时，
最大.
联立方程
，解得
此时
.
购买钾肥70吨，氮肥105吨时，两种肥料的总数量最大为175吨
(Ⅱ)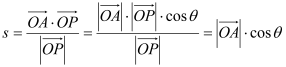
，
，
为
的夹角
.有图可知：
当点
在线段
时，
最大为
，此时s最大值为
；
当点
在线段
时，最小为
，此时s最小值为
.
另解：
，
，代入可得
练习册系列答案
考前必练系列答案
相关题目
