题目内容
【题目】已知关于![]() 的方程为
的方程为![]() .
.
(Ⅰ)若![]() ,
,![]() ,求方程有实数根的概率.
,求方程有实数根的概率.
(Ⅱ)若![]() ,
,![]() ,求方程有实数根的概率.
,求方程有实数根的概率.
(Ⅲ)在区间![]() 上任取两个数
上任取两个数![]() 和
和![]() ,利用随机数模拟的方法近似计算关于
,利用随机数模拟的方法近似计算关于![]() 的方程
的方程![]() 有实数根的概率,请写出你的试验方法.
有实数根的概率,请写出你的试验方法.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)试验方法见解析.
;(III)试验方法见解析.
【解析】
试题分析:(I)由方程有根解出![]() 的范围,端点值之差的绝对值即长度之比即为所求;(II)由方程有根得出
的范围,端点值之差的绝对值即长度之比即为所求;(II)由方程有根得出![]() 的不等式组,在平面直角坐标系中画出图形的可行域,面积之比即为所求;(III)试验的总次数之比即为所求的概率值.
的不等式组,在平面直角坐标系中画出图形的可行域,面积之比即为所求;(III)试验的总次数之比即为所求的概率值.
试题解析:解:(Ⅰ)方程![]() 有实数根等价于
有实数根等价于![]() 即
即![]() , ……1分
, ……1分
由几何概型概率公式得方程有解的概率为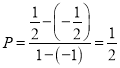 . …………3分
. …………3分
(Ⅱ)方程![]() 有实数根等价于
有实数根等价于![]() .
.![]() 或
或![]() .
.
…………4分
![]() 可看成是平面内的点,试验的所有结果所构成的区域为
可看成是平面内的点,试验的所有结果所构成的区域为![]() ,
,
这是一个正方形区域,面积为![]() , …………6分
, …………6分
设事件![]() ,则
,则![]() 构成的区域为
构成的区域为
![]()
面积为![]() , …………8分
, …………8分
所以由几何概性概率告诉的关于![]() 的方程
的方程![]() 有实数根的概率
有实数根的概率![]() .
.
…………9分
(Ⅲ)第一步:利用计算器或者计算机产生两组0到1之间的随机数:![]() ,
,![]() ;
;
第二步:统计试验的总次数![]() ”的次数
”的次数![]() ;
;
第三步:计算频率![]() ,得出概率的近似值为
,得出概率的近似值为![]() . …………12分
. …………12分

练习册系列答案
相关题目