题目内容
【题目】《情境》刘晓红同学在做达标训练的课外作业时，遇到一个如何用五点法作出正弦型函数在长度为一个周期的闭区间上的图象及图象之间如何进行变换的问题，她犯愁了．
《问题》设函数
的周期为
，且图象过点
．
（1）求
与
的值；
（2）用五点法作函数
在长度为一个周期的闭区间上的图象；
（3）叙述函数的图象可由函数
的图象经过怎样的变换而得到．
由于刘晓红对上述问题还没有掌握解决方法及解题概念和步骤，导致无从下手，于是她请教了班上的学习委员张倩同学给她做了如下点拨：
用五点法作出在一个周期的闭区间上的图象，首先要列表并分别令相位
、
、、
、
，再解出对应的
、
的值，得出坐标
，然后描点，最后画出图象．而由函数的图象变到函数
的图象主要有两种途径：①按物理量初相，周期
，振幅
的顺序变换；②按物理量周期，初相，振幅的顺序变换．要注意两者操作的区别，防止出错．
经过张倩耐心而细致的解释，刘晓红豁然开朗，并对该题解答如下：
（注意：解答第（3）问时，要按照题中要求，写出两种变换过程）
【答案】（1）
，
；（2）见解析；（3）见解析.
【解析】
（1）由函数
的最小正周期计算出
的值，由该函数的图象过点
，结合
的取值范围可求得的值；
（2）分别令相位
、
、
、
、
，再解出对应的
、
的值，得出坐标
，然后列表、描点、连线，可得出函数在长度为一个周期的闭区间上的图象；
（3）利用三角函数图象变换规律可得出题中①②中由函数
变换到函数的变换方法.
（1）由函数
的周期为，且
，知
，解得．
将点代入
中，有
，且
，解得
，
故，；
（2）由（1）知
，
作出函数在一个周期
上的图象．
①列表如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
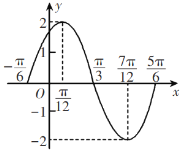
②先描点，再作出函数在一个周期上的图象，如图所示：
③（方法一）先把的图象向左平移
个单位长度，得到
的图象.
再把的图象上所有点的纵坐标不变，横坐标缩短到原来的
，得到
的图象.
最后把的图象上所有点的横坐标不变，纵坐标伸长到原来的
倍，得到
的图象；
（方法二）先将的图象上所有点的纵坐标不变，横坐标变为原来的，得到
的图象，
把的图象向左平移
个单位长度，得到的图象.
最后把的图象上所有点的横坐标不变，纵坐标伸长到原来的倍，得到的图象．
