题目内容
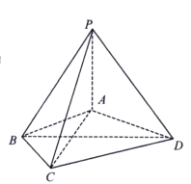
【题目】已知六棱锥
的底面是正六边形，
平面ABC，
.则下列命题中正确的有（ ）
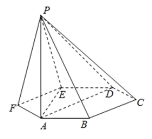
①平面
平面PAE；
②
；
③直线CD与PF所成角的余弦值为
；
④直线PD与平面ABC所成的角为45°；
⑤
平面PAE.
A.①④B.①③④C.②③⑤D.①②④⑤
【答案】B
【解析】
①要判断面面垂直，需先判断是否有线面垂直，根据线线，线面的垂直关系判断；②由条件可知若
，可推出
平面
，则
，判断是否有矛盾；
③异面直线所成的角转化为相交直线所成的角，即根据
，转化为求
；④根据线面角的定义直接求解；⑤若
平面
，则
，由正六边形的性质判断是否有矛盾.
∵
平面ABC，∴
，在正六边形ABCDEF中，
，
，∴
平面PAE，且
面PAB，
∴平面
平面PAE，故①成立；
由条件可知若，平面
，则
，
，可推出平面，则，这与
不垂直矛盾，故②不成立；
∵
，直线CD与PF所成角为
，
在
中，
，
∴
，∴③成立.
在
中，
，
∴
，故④成立.
若平面，平面
平面
则，这与
不平行矛盾，故⑤不成立.
所以正确的是①③④
故选：B
新课标阶梯阅读训练系列答案
【题目】[2019·清远期末]一只红铃虫的产卵数
和温度
有关，现收集了4组观测数据列于下表中，根据数据作出散点图如下：
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |
（1）根据散点图判断
与
哪一个更适宜作为产卵数关于温度的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立关于的回归方程（数字保留2位小数）；
（3）要使得产卵数不超过50，则温度控制在多少
以下？（最后结果保留到整数）
参考数据：
，
，
，
，
，
，
，
，
，
，
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图（甲）所示；依据当地的地质构造，得到水位与灾害等级的频率分布条形图如图（乙）所示．
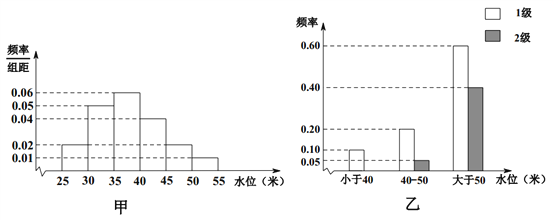
试估计该河流在8月份水位的中位数；
（1）以此频率作为概率，试估计该河流在8月份发生1级灾害的概率；
（2）该河流域某企业，在8月份，若没受1、2级灾害影响，利润为500万元；若受1级灾害影响，则亏损100万元；若受2级灾害影响则亏损1000万元．
现此企业有如下三种应对方案：
方案 | 防控等级 | 费用（单位：万元） |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问，如仅从利润考虑，该企业应选择这三种方案中的哪种方案？说明理由．
