题目内容
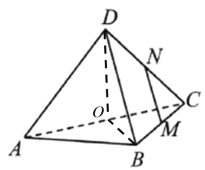
【题目】如图,MN分别是边长为1的正方形ABCD的边BCCD的中点,将正方形沿对角线AC折起,使点D不在平面ABC内,则在翻折过程中,有以下结论:

①异面直线AC与BD所成的角为定值.
②存在某个位置,使得直线AD与直线BC垂直.
③存在某个位置,使得直线MN与平面ABC所成的角为45°.
④三棱锥M-ACN体积的最大值为![]() .
.
以上所有正确结论的序号是__________.
【答案】①③④
【解析】
设![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,得到
,得到![]() 平面
平面![]() ,从而可证①正确;假设
,从而可证①正确;假设![]() ,从而得到
,从而得到![]() 平面
平面![]() ,与已知矛盾,从而证明②错误,根据
,与已知矛盾,从而证明②错误,根据![]() ,得到
,得到![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() ,根据
,根据![]() 的范围,从而证明③正确;
的范围,从而证明③正确;![]() ,从而得到体积最大的情况,求出最大值,可得④正确.
,从而得到体积最大的情况,求出最大值,可得④正确.
设![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
正方形![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,
,
即异面直线![]() 与
与![]() 所成的角为定值
所成的角为定值![]() .
.
故①正确.
若![]() ,而
,而![]() ,
,![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,
,
而![]() 中,
中,![]() ,
,
所以![]() 不可能为直角,故假设错误,
不可能为直角,故假设错误,
所以②错误.
因为![]()
![]() 分别是
分别是![]()
![]() 的中点,所以
的中点,所以![]() ,
,
所以![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角,
所成的角,
![]() 在平面
在平面![]() 的射影在
的射影在![]() 上,
上,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
而![]() ,所以一定存在某个位置满足
,所以一定存在某个位置满足![]() ,
,
即存在某个位置,使得直线MN与平面所成的角为45°.
故③正确;
![]() ,底面
,底面![]() ,
,
所以当平面![]() 平面
平面![]() 时,
时,![]() 到平面
到平面![]() 的距离最大,
的距离最大,
此时三棱锥![]() 的体积最大,
的体积最大,
![]() ,
,
所以此时![]() ,
,
故④正确.
故答案为:①③④

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】已知具有线性相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(2)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求恰有1个点落在直线![]() 右下方的概率.
右下方的概率.
参考公式: 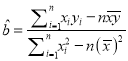 ,
, ![]() .
.