题目内容
【题目】已知F1 ， F2为椭圆 
的左、右焦点，F2在以 
为圆心，1为半径的圆C2上，且|QF1|+|QF2|=2a．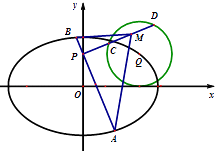
（1）求椭圆C1的方程；
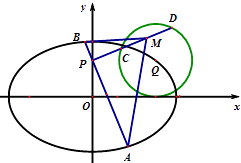
（2）过点P（0，1）的直线l1交椭圆C1于A，B两点，过P与l1垂直的直线l2交圆C2于C，D两点，M为线段CD中点，求△MAB面积的取值范围．
【答案】
（1）
解：圆C2的方程为 
，
此圆与x轴相切，切点为 
∴ 
，即a2﹣b2=2，且 
， 
又|QF1|+|QF2|=3+1=2a．
∴a=2，b2=a2﹣c2=2
∴椭圆C1的方程为 
．
（2）
解：当l1平行x轴的时候，l2与圆C2无公共点，从而△MAB不存在；
设l1：x=t（y﹣1），则l2：tx+y﹣1=0．
由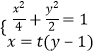 
，消去x得（t2+2）y2﹣2t2y+t2﹣4=0，
则 
．
又圆心 
到l2的距离 
，得t2＜1．
又MP⊥AB，QM⊥CD
∴M到AB的距离即Q到AB的距离，设为d2，
即 
．
∴△MAB面积 
令 
则 
．
∴△MAB面积的取值范围为 
．
【解析】（1）圆C2的方程为 ，由此圆与x轴相切，求出a，b的值，由此能求出椭圆C1的方程．（2）设l1：x=t（y﹣1），则l2：tx+y﹣1=0，与椭圆联立，得（t2+2）y2﹣2t2y+t2﹣4=0，由此利用弦长公式、点到直线距离公式，结合已知条件能求出△MAB面积的取值范围．
练习册系列答案
相关题目
