题目内容
已知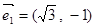 ,
, ,若
,若 ,
, ,若
,若 ,则实数
,则实数 和
和 满足的一个关系式是 ,
满足的一个关系式是 , 的最小值为 .
的最小值为 .
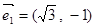 ,
, ,若
,若 ,
, ,若
,若 ,则实数
,则实数 和
和 满足的一个关系式是 ,
满足的一个关系式是 , 的最小值为 .
的最小值为 .本试题主要是考查了向量的数量积公式的运用和函数的 最值的求解。
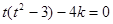 ,
,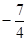 。
。
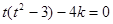 ,
,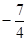 。
。 因为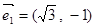 ,
, ,若
,若 ,
, ,且有
,且有 ,那么数量积为零,即
,那么数量积为零,即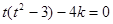 ,那么可知k,t的关系式,
,那么可知k,t的关系式,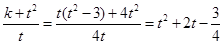 ,结合二次函数性质可知
,结合二次函数性质可知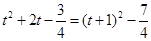 最小值为
最小值为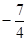 。
。
解决该试题的关键是利用垂直关系得到k,t的关系式,然后消元法得到函数关系式进而求解最值。
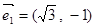 ,
, ,若
,若 ,
, ,且有
,且有 ,那么数量积为零,即
,那么数量积为零,即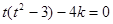 ,那么可知k,t的关系式,
,那么可知k,t的关系式,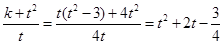 ,结合二次函数性质可知
,结合二次函数性质可知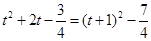 最小值为
最小值为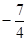 。
。解决该试题的关键是利用垂直关系得到k,t的关系式,然后消元法得到函数关系式进而求解最值。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
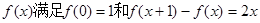 .
.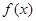 的解析式;
的解析式;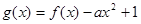 有一个正的零点,求实数
有一个正的零点,求实数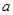 的取值范围。
的取值范围。

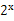 -2,若同时满足条件:
-2,若同时满足条件: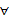 x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;②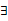 x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。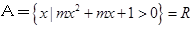 ,求实数
,求实数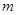 的取值范围;
的取值范围;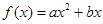 ,满足
,满足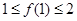 ,
,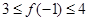 ,求
,求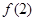 的取值范围.
的取值范围. 对任意实数
对任意实数 都有
都有 ,那么( )
,那么( )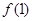 <
< <
<
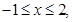 则
则 的最大值与最小值之差为 .
的最大值与最小值之差为 .