题目内容
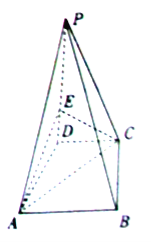
【题目】如图,在四棱锥![]() 中,
中,![]()
![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
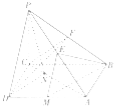
(1)求证:![]() ;
;
(2)已知点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一动点,当
上一动点,当![]() 为何值时,平面
为何值时,平面![]() ?
?
【答案】(1)证明见解析;(2)当![]() 时,平面
时,平面![]() .
.
【解析】
试题分析:(1)根据线面垂直的判定定理,若证![]() 平面
平面![]() ,则须证
,则须证![]() 垂直于平面
垂直于平面![]() 内的两条相交直线.根据题意,易证
内的两条相交直线.根据题意,易证![]() ,
,![]() ,又
,又![]() ,从而问题可得证;(2)根据题意,过点
,从而问题可得证;(2)根据题意,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,因为
,因为![]() 是
是![]() 的中点,所以易证平面
的中点,所以易证平面![]() 平面
平面![]() ,即平面
,即平面![]() 平面
平面![]() ,又在矩形
,又在矩形![]() 中,易求得
中,易求得![]() ,当
,当![]() 是
是![]() 与
与![]() 的交点时,即
的交点时,即![]() 时,平面
时,平面![]() .
.
试题解析:(1)证明:∵![]() ,底面
,底面![]() 是矩形,
是矩形,
∴![]() ,又
,又![]() ,∴
,∴![]() ,………………2分
,………………2分
∴![]() .………………………………………………4分
.………………………………………………4分
∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() .………………………………5分
.………………………………5分
∵![]() ,∴
,∴![]() .……………………………………6分
.……………………………………6分
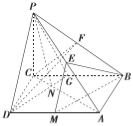
(2)过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,………………………………7分
,………………………………7分
∵∴![]() ,……………………………………8分
,……………………………………8分
∵![]() ,∴
,∴![]() ,……………………………………9分
,……………………………………9分
∴当![]() 是
是![]() 与
与![]() 的交点时,平面
的交点时,平面![]() ,…………………………………………10分
,…………………………………………10分
在矩形![]() 中,求得
中,求得![]() .……………………………………12分
.……………………………………12分

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目