题目内容
【题目】已知椭圆
的离心率为
，以
为圆心，椭圆的短半轴长为半径的圆与直线
相切.
（1）求椭圆
的标准方程；
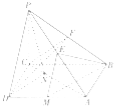
（2）已知点
，和面内一点
，过点
任作直线
与椭圆
相交于
两点，设直线
的斜率分别为
，若
，试求
满足的关系式.
【答案】（1） 
；（2）
.
【解析】
试题分析：（1）
，并且
与直线
相切，那么圆心到直线的距离
，再根据
，计算
得到椭圆的标准方程；（2）当斜率不存在时，求出A,B两点的坐标，分别计算
，代入公式
，得到
的关系式，当斜率存在时，设出直线方程，与椭圆方程联立，得到根与系数的关系，并且表示
，当满足，得到的关系式.
试题解析：（1）
（2）①当直线斜率不存在时，由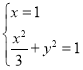
，解得
，不妨设
，
，
因为
，所以
，所以
的关系式为
.
②当直线的斜率存在时，设点
，设直线
，联立椭圆整理得：
，根系关系略，所以
所以
，所以
的关系式为.
练习册系列答案
相关题目
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
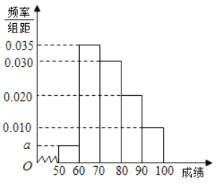
（1）求图中
的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
