题目内容
13.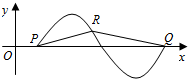 已知函数f(x)=2sin($\frac{π}{4}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象图象与x轴的交点分别为点P,Q(如图所示),图象上的点R的坐标为(4,$\sqrt{2}$).
已知函数f(x)=2sin($\frac{π}{4}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象图象与x轴的交点分别为点P,Q(如图所示),图象上的点R的坐标为(4,$\sqrt{2}$).(1)求函数f(x)的解析式,并求函数f(x)的值域;
(2)求向量$\overrightarrow{PR}$与$\overrightarrow{PQ}$的夹角的余弦值.
分析 (1)把(4,$\sqrt{2}$)代入已知解析式可得φ值,可得解析式,可得值域;
(2)由(1)可得P(1,0)和Q(9,0),可得向量坐标,由夹角公式可得.
解答 解:(1)由题意把(4,$\sqrt{2}$)代入f(x)=2sin($\frac{π}{4}$x+φ)可得$\sqrt{2}$=2sin(π+φ),
∴sinφ=-$\frac{\sqrt{2}}{2}$,又|φ|<$\frac{π}{2}$,∴φ=-$\frac{π}{4}$,∴f(x)=2sin($\frac{π}{4}$x-$\frac{π}{4}$),
∴函数f(x)的值域为[-2,2];
(2)由(1)可得f(x)=2sin($\frac{π}{4}$x-$\frac{π}{4}$),
令2sin($\frac{π}{4}$x-$\frac{π}{4}$)=0可得$\frac{π}{4}$x-$\frac{π}{4}$=kπ,解得x=4k+1,k∈Z
结合图象可取k=0得P(1,0),取k=2可得Q(9,0),
∴$\overrightarrow{PR}$=(3,$\sqrt{2}$),$\overrightarrow{PQ}$=(8,0),
∴向量$\overrightarrow{PR}$与$\overrightarrow{PQ}$的夹角的余弦值cosθ=$\frac{\overrightarrow{PR}•\overrightarrow{PQ}}{|\overrightarrow{PR}||\overrightarrow{PQ}|}$=$\frac{24}{8\sqrt{11}}$=$\frac{3\sqrt{11}}{11}$
点评 本题考查正弦函数的图象和性质,涉及向量的夹角公式,属中档题.

 名校课堂系列答案
名校课堂系列答案| A. | an=2n+1 | B. | an=2n-1 | C. | an=2n-3 | D. | an=2n+3 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |