题目内容
1.若函数f(x)=logm(m-x)在区间[3,5]上的最大值比最小值大1,则实数m=3$+\sqrt{6}$.分析 分类讨论0<m<1时,函数f(x)=logm(m-x)是单调递增函数,得出函数的最大值,最小值,得出方程logm(m-5)-logm(m-3)=1,
m>1时,函数f(x)=logm(m-x)是单调递减函数,logm(m-3)-logm(m-5)=1,求解即可.
解答 解:①∵0<m<1时,函数f(x)=logm(m-x)是单调递增函数,
∴logm(m-5)-logm(m-3)=1,
即$\frac{m-5}{m-3}$=m,(m-2)2+1=0,无解;
②∵m>1时,函数f(x)=logm(m-x)是单调递减函数,
∴logm(m-3)-logm(m-5)=1,
$\frac{m-3}{m-5}$=m,
即m2-6m+3=0,
m=3$±\sqrt{6}$,
∵m-3>0,m-5>0,
∴m>5,
∴m=3$+\sqrt{6}$符合题意,
故答案为;3$+\sqrt{6}$.
点评 本题考查了分类讨论思想的运用,函数的单调性,方程的求解属于综合题,属于中档题.

练习册系列答案
相关题目
9.不等式(x+3)2<1的解集是( )
| A. | {x|x>-2} | B. | {x|x<-4} | C. | {x|-4<x<-2} | D. | {x|-4≤x≤-2} |
16.已知x,y是正数,且xy=4,则$\frac{y}{\sqrt{x}}$+$\frac{x}{\sqrt{y}}$取得最小值时,x的值是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
6.设集合A={x|x2-2x≤0,x∈R},B={x|x≥a},若A∪B=B,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
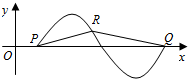 已知函数f(x)=2sin($\frac{π}{4}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象图象与x轴的交点分别为点P,Q(如图所示),图象上的点R的坐标为(4,$\sqrt{2}$).
已知函数f(x)=2sin($\frac{π}{4}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象图象与x轴的交点分别为点P,Q(如图所示),图象上的点R的坐标为(4,$\sqrt{2}$).