题目内容
5.已知A(a,b)在直线y=-2x+1上,其中a>0,b>0,则ab的最大值是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{2}$ |
分析 由题意和直线的知识可得正数a和b满足2a+b=1,可得ab=$\frac{1}{2}$•2a•b≤$\frac{1}{2}$$(\frac{2a+b}{2})^{2}$=$\frac{1}{8}$,验证等号成立即可.
解答 解:∵A(a,b)在直线y=-2x+1上,其中a>0,b>0,
∴b=-2a+1,即2a+b=1,
∴ab=$\frac{1}{2}$•2a•b≤$\frac{1}{2}$$(\frac{2a+b}{2})^{2}$=$\frac{1}{8}$
当且仅当2a=b即a=$\frac{1}{4}$且b=$\frac{1}{2}$时取等号,
∴ab的最大值是$\frac{1}{8}$,
故选:C.
点评 本题考查基本不等式求最值,凑出可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
相关题目
11.条件p:x1是方程f(x)=0的一个根,或x1是方程g(x)=0的一个根;条件q:x1是方程f(x)•g(x)=0的一个根.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
16.已知x,y是正数,且xy=4,则$\frac{y}{\sqrt{x}}$+$\frac{x}{\sqrt{y}}$取得最小值时,x的值是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
20.设等差数列{an}的前n项和为Sn.若以a2,a4是方程x2-4x+3=0的两个根,则S5等于( )
| A. | -20 | B. | -10 | C. | 10 | D. | 20 |
 已知函数f(x)=2sin($\frac{π}{4}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象图象与x轴的交点分别为点P,Q(如图所示),图象上的点R的坐标为(4,$\sqrt{2}$).
已知函数f(x)=2sin($\frac{π}{4}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象图象与x轴的交点分别为点P,Q(如图所示),图象上的点R的坐标为(4,$\sqrt{2}$).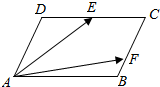 如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.
如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.