题目内容
4．计算：tan1°•tan2•tan3°•…•tan89°．分析 由诱导公式可得tan1°tan89°=tan2°tan88°=…=tan44°tan46°=1，可得答案．
解答 解：∵tan89°=tan（90°-1°）=$\frac{sin（90°-1°）}{cos（90°-1°）}$=$\frac{cos1°}{sin1°}$=$\frac{1}{tan1°}$，
∴tan1°tan89°=1，
同理可得tan2°tan88°=1，…，tan44°tan46°=1
又tan45°=1
∴原式=1
点评 本题考查诱导公式，寻找式子的规律是解决问题的关键，属基础题．
练习册系列答案
相关题目
11．条件p：x1是方程f（x）=0的一个根，或x1是方程g（x）=0的一个根；条件q：x1是方程f（x）•g（x）=0的一个根．则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
9．不等式（x+3）2＜1的解集是（ ）
| A． | {x|x＞-2} | B． | {x|x＜-4} | C． | {x|-4＜x＜-2} | D． | {x|-4≤x≤-2} |
16．已知x，y是正数，且xy=4，则$\frac{y}{\sqrt{x}}$+$\frac{x}{\sqrt{y}}$取得最小值时，x的值是（ ）
| A． | 1 | B． | 2 | C． | 2$\sqrt{2}$ | D． | $\sqrt{2}$ |
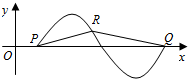已知函数f（x）=2sin（$\frac{π}{4}$x+φ）（|φ|＜$\frac{π}{2}$）的部分图象图象与x轴的交点分别为点P，Q（如图所示），图象上的点R的坐标为（4，$\sqrt{2}$）．