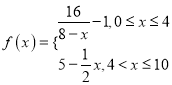题目内容
【题目】函数![]() 对任意
对任意![]() 都有
都有![]() ,则称
,则称![]() 为在区间
为在区间![]() 上的可控函数,区间
上的可控函数,区间![]() 称为函数
称为函数![]() 的“可控”区间,写出函数
的“可控”区间,写出函数![]() 的一个“可控”区间是________.
的一个“可控”区间是________.
【答案】![]() 的子集都可以
的子集都可以
【解析】
由![]() ,由可控函数的定义可得
,由可控函数的定义可得![]() ,即
,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 运算即可得解.
运算即可得解.
解:因为![]() ,所以
,所以![]() ,
,
由可控函数的定义可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
又![]()
即![]() 即
即![]()
则区间![]() 可为
可为![]() ,
,
即函数![]() 的一个“可控”区间是
的一个“可控”区间是![]() ,
,
故答案为: ![]() .
.
【点晴】
本题以函数的形式为背景,考查的是不等式的有关知识及推理判断的能力.结论的开放性和不确定性是本题的一大特色.解答时应充分依据题设条件,合理有效地利用好可控函数及可控区间等新信息和新定义,并以此为基础进行推理论证,从而写出满足题设条件的答案.解答本题时,借助绝对值不等式的性质进行巧妙推证,从而探寻出符合题设条件的一可控区间的区间.

练习册系列答案
相关题目