题目内容
【题目】某厂需要确定加工某大型零件所花费的时间，连续4天做了4次统计，得到的数据如下：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 5.5 |
（1）在直角坐标系中画出以上数据的散点图，求出
关于
的回归方程
，并在坐标系中画出回归直线；
（2）试预测加工10个零件需要多少时间？
参考公式：两个具有线性关系的变量的一组数据：
，
其回归方程为，其中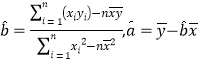
【答案】(1)
,图见解析;（2）8.05小时.
【解析】试题分析：（1）在表中描出
，分别算出
，代入公式，可求得
和
（2）由（1）中求出线性回归方程，代入x=10,即求。
试题解析：（1）由表中数据可得
， 
， 
，
，
所以，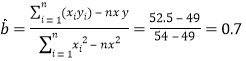
所以，
，
所求回归方程为．
在坐标系中画出回归直线如图：
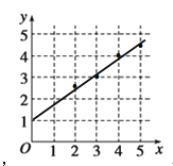
（2）由（1）得到的回归方程，将
代入回归直线方程得
所以，预测加工10个零件需8.05小时.
练习册系列答案
相关题目
【题目】已知函数
的定义域为
，部分对应值如下表，又知
的导函数
的图象如下图所示：
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
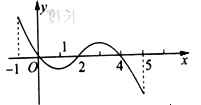
则下列关于
的命题：
①函数
的极大值点为2；
②函数
在
上是减函数；
③如果当
时， 
的最大值是2，那么
的最大值为4；
④当
，函数
有4个零点.
其中正确命题的序号是__________．
