题目内容
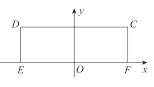
【题目】已知长方形![]() ,
, ![]() ,
, ![]() ,以
,以![]() 的中点
的中点![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系![]() .
.
(1)求以![]() 为焦点,且过
为焦点,且过![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点![]() 作直线
作直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,设
,设![]() ,点
,点![]() 坐标为
坐标为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)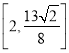 .
.
【解析】试题分析:(1)确定![]() 的坐标,利用椭圆的定义,求出几何量,即可求椭圆的标准方程;(2)设出直线方程,代入椭圆方程,利用韦达定理及向量知识,结合配方法,即可求
的坐标,利用椭圆的定义,求出几何量,即可求椭圆的标准方程;(2)设出直线方程,代入椭圆方程,利用韦达定理及向量知识,结合配方法,即可求![]() 的取值范围.
的取值范围.
试题解析:(1)由题意可得点![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,
, 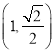 .设椭圆的标准方程是
.设椭圆的标准方程是![]() ,则
,则![]() ,∴
,∴![]() .∴
.∴![]() ,∴椭圆的标准方程为
,∴椭圆的标准方程为![]() .
.

(2)由题意容易验证直线![]() 的斜率不为0,故可设直线
的斜率不为0,故可设直线![]() 的方程为
的方程为![]() .代入
.代入![]() 中,得
中,得![]() .设
.设![]() ,
, ![]() ,由根与系数关系,得
,由根与系数关系,得![]() ①,
①,![]() ②,∵
②,∵![]() ,∴
,∴![]() 且
且![]() ,将上式①的平方除以②,得
,将上式①的平方除以②,得![]() ,即
,即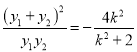 ,所以
,所以![]() ,由
,由![]()
![]() ,即
,即![]() .∵
.∵![]() ,
, ![]() ,
, ![]() ,又
,又![]() ,
, ![]() .故
.故![]()
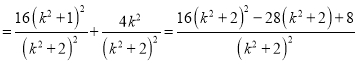
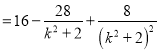 .令
.令![]() ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,
, 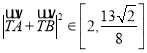 .
.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中![]() 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.
(1)请你根据已知的数据,填写下列![]() 列联表:
列联表:
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | |||
不常使用单车用户 | |||
合计 |
(2)请根据(1)中的列联表,计算![]() 值并判断能否有
值并判断能否有![]() 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?
(附: 
当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关;当
有关;当![]() 时,认为事件
时,认为事件![]() 与
与![]() 是无关的)
是无关的)
【题目】在一次抽样调查中测得样本的6组数据,得到一个变量![]() 关于
关于![]() 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数![]() 加以说明
加以说明![]() 与
与![]() 之间存在线性相关关系(当
之间存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 关于
关于![]() 的回归方程并预测当
的回归方程并预测当![]() 时,对应的
时,对应的![]() 值为多少(
值为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
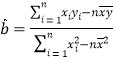 ,
,![]() ,相关系数
,相关系数![]() 公式为:
公式为: .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于25”的概率;
均小于25”的概率;
(2)请根据3月2日至3月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)所得的线性回归方程是否可靠?
(参考公式:回归直线方程为![]() ,其中
,其中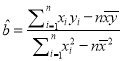 ,
, ![]() )
)