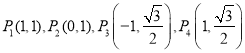题目内容
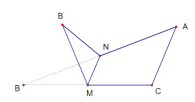
【题目】如图,∠C=![]() ,
,![]() ,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为
,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由∠C=![]() ,
,![]() ,先得到∠B′ND就为斜线B′N与平面ABC所成的角设为α,设BC=2,AC=
,先得到∠B′ND就为斜线B′N与平面ABC所成的角设为α,设BC=2,AC=![]() ,BM=B'M=1,DM=B'Mcos60°=
,BM=B'M=1,DM=B'Mcos60°=![]() ,B'D=B'Msin60°=
,B'D=B'Msin60°=![]() ,又MN=
,又MN=![]() ,所以DN=
,所以DN=![]() ,所以tanα=
,所以tanα=![]() ,解出即可.
,解出即可.
解:∵∠C=![]() ,
,![]() ,M、N分别是BC、AB的中点,
,M、N分别是BC、AB的中点,
将△BMN沿直线MN折起,使二面角B′-MN-B的大小为![]() .∴∠BMB′=
.∴∠BMB′=![]() ,
,
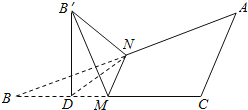
取BM的中点D,连B′D,ND,
由于折叠之前BM与CM都始终垂直于MN,这在折叠之后仍然成立,
∴折叠之后平面B′MN与平面BMN所成的二面角即为∠B′MD=60°,
并且B′在底面ACB内的投影点D就在BC上,∴B′D⊥BC,B′D⊥AD,B′D⊥面ABC,
∴∠B′ND就为斜线B′N与平面ABC所成的角设为α,
设BC=2,AC=![]() ,BM=B'M=1,DM=B'Mcos60°=
,BM=B'M=1,DM=B'Mcos60°=![]() ,B'D=B'Msin60°=
,B'D=B'Msin60°=![]() ,
,
又MN=![]() ,所以DN=
,所以DN=![]() ,
,
所以tanα=![]() =
=![]() =
=![]() .
.
故选C.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目