题目内容
16.设等差数列{an}的前n项和为Sn,若S11>0,S12<0,则$\frac{{S}_{1}}{{a}_{1}}$,$\frac{{S}_{2}}{{a}_{2}}$,…$\frac{{S}_{11}}{{a}_{11}}$中最大的是$\frac{{S}_{6}}{{a}_{6}}$.分析 由题意和等差数列的性质以及求和公式可得等差数列的前6项为正数,从第7项开始为负数,数列的前6项和最大,可得结论.
解答 解:由S11=$\frac{11({a}_{1}+{a}_{11})}{2}$=$\frac{11×2{a}_{6}}{2}$=11a6>0,∴a6>0,
同理可得S12=$\frac{12({a}_{1}+{a}_{12})}{2}$=$\frac{12({a}_{6}+{a}_{7})}{2}$=6(a6+a7)<0,
∴a6+a7<0,结合a6>0可得a7<0,
∴等差数列的前6项为正数,从第7项开始为负数,
∴数列的前6项和最大,
故$\frac{{S}_{1}}{{a}_{1}}$,$\frac{{S}_{2}}{{a}_{2}}$,…$\frac{{S}_{11}}{{a}_{11}}$中最大的是$\frac{{S}_{6}}{{a}_{6}}$,
故答案为:$\frac{{S}_{6}}{{a}_{6}}$.
点评 本题考查等差数列的求和公式和最值,从数列项的正负入手是解决问题的关键,属基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.双曲线x2-4my2=4的实轴长是虚轴长的2倍,则实数m=( )
| A. | 1 | B. | $\frac{1}{16}$ | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{16}$ |
7.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
1.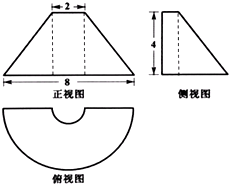 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )| A. | 12+$\frac{47π}{2}$ | B. | 12+23π | C. | 12+24π | D. | 12+$\frac{45}{2}$π |
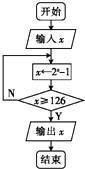
5.执行如图所示的程序框图,则输出的结果为( )


| A. | 2 | B. | 1 | C. | -1 | D. | -2 |