题目内容
已知递增的等比数列{an}的前三项之积为512,且这三项分别依次减去1、3、9后又成等差数列.
(1)求数列{an}的通项公式;
(2)若Tn=
+
+
+…+
,求Tn.
(1)求数列{an}的通项公式;
(2)若Tn=
| 1 |
| a1 |
| 2 |
| a2 |
| 3 |
| a3 |
| n |
| an |
(1)设递增的等比数列{an}的前三项分别为a1,a2,a3,
则a1a2a3=512,∴a2=8.
又这三项分别依次减去1、3、9后又成等差数列,
则2(a2-3)=a1-1+a3-9,即a1+a3=20.
又∵a1a3=a22=64,且a1<a3,∴a1=4,a3=16,
∴等比数列{an}的公比q=2.
∴an=a1qn-1=4•2n-1=2n+1;
(2)证明:令bn=
=
=n(
)n+1,
则Tn=b1+b2+…+bn
=1•(
)2+2•(
)3+…+(n-1)•(
)n+n•(
)n+1,①
Tn=(
)3+2•(
)4+…+(n-1)•(
)n+1+n•(
)n+2,②
①-②得:
Tn=(
)2+(
)3+…+(
)n+1-n•(
)n+2,
即Tn=
+(
)2+…+(
)n-n•(
)n+1,
∴Tn=
-n•(
)n+1=1-(1+
)•(
)n.
则a1a2a3=512,∴a2=8.
又这三项分别依次减去1、3、9后又成等差数列,
则2(a2-3)=a1-1+a3-9,即a1+a3=20.
又∵a1a3=a22=64,且a1<a3,∴a1=4,a3=16,
∴等比数列{an}的公比q=2.
∴an=a1qn-1=4•2n-1=2n+1;
(2)证明:令bn=
| n |
| an |
| n |
| 2n+1 |
| 1 |
| 2 |
则Tn=b1+b2+…+bn
=1•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=
| ||||
1-
|
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 =" " ( )
=" " ( ) C 1 D
C 1 D 
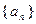 的首项
的首项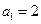 ,公比
,公比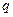 是最小的正整数,则数列
是最小的正整数,则数列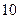 项的和为
项的和为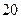 B
B 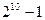 C
C 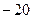 D
D 
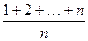 ,bn=
,bn=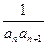 ,则{bn}的前n项
,则{bn}的前n项