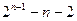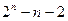题目内容
已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,则 =" " ( )
=" " ( )
A 2 B C 1 D
C 1 D 
 =" " ( )
=" " ( )A 2 B
 C 1 D
C 1 D 
C
因为数列{log2(an-1)}(n∈N*)为等差数列,∴
故设log2(an+1-1)-log2(an-1)=d
又a1=3,a2=5,故d=1
∴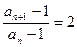 ,
,
故{an-1}是首项为2,公比为2的等比数列,
∴an-1=2n,∴an=2n+1,∴an+1-an=2n
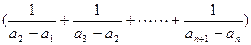 =
=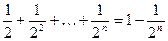
则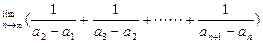 =1
=1
故设log2(an+1-1)-log2(an-1)=d
又a1=3,a2=5,故d=1
∴
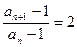 ,
,故{an-1}是首项为2,公比为2的等比数列,
∴an-1=2n,∴an=2n+1,∴an+1-an=2n
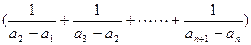 =
=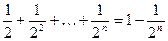
则
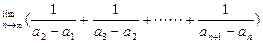 =1
=1
练习册系列答案
相关题目
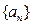 ,
,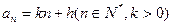 ,数列
,数列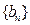 定义如下:对于正整数
定义如下:对于正整数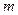
 是使不等式
是使不等式 成立的所有
成立的所有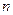 中的最小值
中的最小值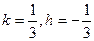 ,求
,求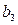
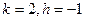 ,求数列
,求数列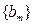 的前
的前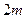 项和
项和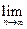
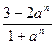 的值是 .
的值是 . ).
).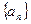 中,
中,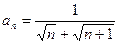 ,若前
,若前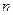 项和
项和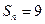 ,则项数
,则项数

 的结果为( )
的结果为( )