题目内容
a、b是不互相垂直的异面直线，α、β是分别过a、b的平面，则下列四种情况：
①α∥β；②α⊥β；③a∥β；④a⊥β，
其中可能出现的有（ ）
①α∥β；②α⊥β；③a∥β；④a⊥β，
其中可能出现的有（ ）
| A、1种 | B、2种 | C、3种 | D、4种 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：由异面直线的定义，线面平行的判定定理、面面平行的定义和面面垂直的性质定理判断．
解答：
解：①可能，过a上一点作与b平行的直线确定的平面α，则b∥α，过b上一点作与a平行的直线确定的平面β，则a∥β，由面面平行的定义知；
②可能，面面垂直的性质定理，当α⊥β可以找到两条直线异面，故②可能；
③可能，过a上一点作与b平行的直线确定的平面β，则a∥β；
④不可能，如果a⊥β，由面面垂直的性质可得a⊥b，与a与b不垂直矛盾；
故选C．
②可能，面面垂直的性质定理，当α⊥β可以找到两条直线异面，故②可能；
③可能，过a上一点作与b平行的直线确定的平面β，则a∥β；
④不可能，如果a⊥β，由面面垂直的性质可得a⊥b，与a与b不垂直矛盾；
故选C．
点评：本题主要考查了异面直线的位置关系，利用线面平行的判定定理、面面平行的定义和面面垂直的性质定理，注重学生对定理的运用能力和空间想象能力的培养．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
椭圆
+
=1上的点M到左焦点F1的距离是2，N是MF1的中点，O为坐标原点，则|ON|为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
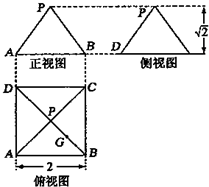某几何体的三视图如图所示，P是正方形ABCD对角线的交点，G是PB的中点．