题目内容
13.设函数f(x)=x2-mx+2(m∈R),若当x>1时,f(x)≥0恒成立,则m的取值范围为(-∞,2$\sqrt{2}$].分析 依题意得:m≤x+$\frac{2}{x}$,构造函数g(x)=x+$\frac{2}{x}$(x>1),利用导数法可求得g(x)min=g($\sqrt{2}$)=2$\sqrt{2}$,从而可求得m的取值范围.
解答 解:∵x>1,∴m≤x+$\frac{2}{x}$,
令g(x)=x+$\frac{2}{x}$(x>1),
则m≤g(x)min.
g′(x)=$\frac{(x-\sqrt{2})(x+\sqrt{2})}{{x}^{2}}$,
∵x>1,
当x∈(1,$\sqrt{2}$)时,g′(x)<0,y=g(x)在区间(1,$\sqrt{2}$)上单调递减,
当x∈($\sqrt{2}$,2)时,g′(x)>0,y=g(x)在区间($\sqrt{2}$,2)上单调递增,
∴当x=$\sqrt{2}$时,g(x)=x+$\frac{2}{x}$取得极小值,也是区间(1,2)上的最小值,
即g(x)min=g($\sqrt{2}$)=2$\sqrt{2}$,
∴m≤2$\sqrt{2}$.
故答案为:(-∞,2$\sqrt{2}$].
点评 本题考查函数恒成立问题,着重考查利用导数法求极值,考查构造函数思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
8.奇函数f(x)在(0,+∞)上单调递减且f(-2)=0,则满足xf(x)>0的x的范围是( )
| A. | x<-2或0<x<2 | B. | x<-2或x>2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
18.函数y=2-x-1+1的图象可以由函数y=2-x的图象( )
| A. | 先向右平移1个单位,再向上平移1个单位得到 | |
| B. | 先向左平移1个单位,再向上平移1个单位得到 | |
| C. | 先向右平移1个单位,再向下平移1个单位得到 | |
| D. | 先向左平移1个单位,再向下平移1个单位得到 |
2.圆的一条直径为x=2(-2≤y≤0),则此圆的方程是( )
| A. | (x-2)2+(y-1)2=1 | B. | (x-2)2+(y+1)2=1 | C. | (x+2)2+(y-1)2=1 | D. | (x+2)2+(y+1)2=1 |
3.函数y=$\frac{2x}{lnx}$的图象大致为( )
| A. |  | B. | 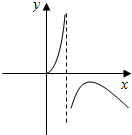 | C. | 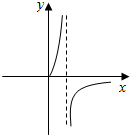 | D. |  |