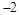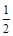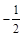题目内容
本题满分10分)
设函数
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线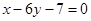 垂直,导函数
垂直,导函数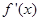 的最小值为
的最小值为 .试求
.试求 ,
,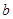 ,
, 的值。
的值。
设函数

 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线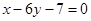 垂直,导函数
垂直,导函数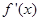 的最小值为
的最小值为 .试求
.试求 ,
,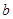 ,
, 的值。
的值。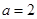 ,
,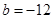 ,
, .
.试题分析:由y=f(x)为奇函数,知c=0,故f(x)=ax3+bx,所以f'(x)=3ax2+b,f'(1)=3a+b=-6,由导数f'(x)的 最小值为-12,知b=-12,由此能求出a,b,c的值.
解:∵
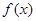 为奇函数,∴
为奇函数,∴
即
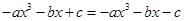 ∴
∴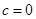 (4分)
(4分)∵
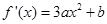 的最小值为
的最小值为 ∴
∴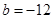 (6分)
(6分)又直线
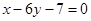 的斜率为
的斜率为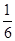 因此,
因此,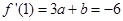 (8分)
(8分)∴
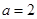 ,
,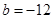 ,
,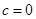 .(10分)
.(10分)点评:解决该试题的关键是理解导数几何意义的运用明确导数的值即为该点处的切线的斜率,只要只要点的坐标和导数值,既可以写出切线方程。

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
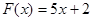 (
(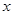 单位为
单位为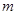 ,
,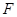 单位为
单位为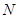 )的作用下,沿着与力
)的作用下,沿着与力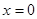 处运动到
处运动到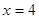 处,则力
处,则力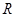 上的函数
上的函数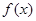 满足
满足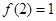 ,且
,且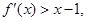 则不等式
则不等式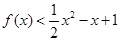 的解集为( )
的解集为( )

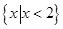
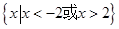
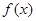 满足
满足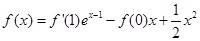 ,则
,则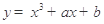 相切于点A(1,3)则b的值为
相切于点A(1,3)则b的值为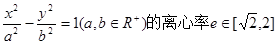 ,则一条渐近线与实轴所构成的角的取值范围是 .
,则一条渐近线与实轴所构成的角的取值范围是 .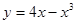 在点(-1,-3)处的切线方程是
在点(-1,-3)处的切线方程是 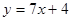
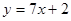
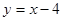
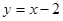
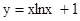
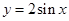 在点
在点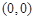 处的切线与直线
处的切线与直线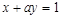 垂直,则实数
垂直,则实数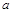 的值为( )
的值为( )