题目内容
19.若f(x)=$\frac{1}{2}$(x+|x|),则f(f(x))是( )| A. | x+|x| | B. | 0 | C. | $\left\{\begin{array}{l}{x,x≤0}\\{0,x>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x,x≥0}\\{0,x<0}\end{array}\right.$ |
分析 先去绝对值号得到f(x)=$\left\{\begin{array}{l}{x}&{x≥0}\\{0}&{x<0}\end{array}\right.$,这样x≥0时,f(x)=x,从而f(f(x))=f(x)=x,同样求出x<0时的f(f(x)),这样便可写出f(f(x))的解析式.
解答 解:$f(x)=\left\{\begin{array}{l}{x}&{x≥0}\\{0}&{x<0}\end{array}\right.$;
∴$f(f(x))=\left\{\begin{array}{l}{x}&{x≥0}\\{0}&{x<0}\end{array}\right.$.
故选D.
点评 考查含绝对值函数的处理方法:去绝对值号,若f(x)为分段函数,在求f(f(x))时,要在每一段函数上求.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若α=n•360°+θ,β=m•360°-θ,m,n∈Z,则α,β终边的位置关系是( )
| A. | 重合 | B. | 关于原点对称 | C. | 关于x轴对称 | D. | 关于y轴对称 |
11.已知函数f($\frac{x+1}{2}$)=x2-2x,则函数f(x)在[-1,2)上的值域为( )
| A. | [-1,15] | B. | [-1,3) | C. | [-3,3) | D. | (3,15] |
8.如图,△ABC中,D,E分别为AB,AC的中点,CD与BE交于F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$,则m+n=( )
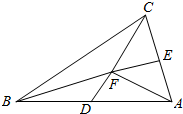

| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
9.已知0<a<1,方程(x-a)(x-$\frac{1}{a}$)=0的解是( )
| A. | -a,a | B. | a,$\frac{1}{a}$ | C. | -a,$\frac{1}{a}$ | D. | -$\frac{1}{a}$,a |