题目内容
9．已知0＜a＜1，方程（x-a）（x-$\frac{1}{a}$）=0的解是（ ）| A． | -a，a | B． | a，$\frac{1}{a}$ | C． | -a，$\frac{1}{a}$ | D． | -$\frac{1}{a}$，a |
分析 直接利用才求解根即可．
解答 解：0＜a＜1，方程（x-a）（x-$\frac{1}{a}$）=0的解是x=a或x=$\frac{1}{a}$．
故选：B．
点评 本题考查函数的零点与方程的根的关系，考查计算能力．
练习册系列答案
相关题目
19．若f（x）=$\frac{1}{2}$（x+|x|），则f（f（x））是（ ）
| A． | x+|x| | B． | 0 | C． | $\left\{\begin{array}{l}{x，x≤0}\\{0，x＞0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x，x≥0}\\{0，x＜0}\end{array}\right.$ |
20．方程x2-6px+p2=0有两个实数根x1、x2，则$\frac{1}{{x}_{1}+p}$+$\frac{1}{{x}_{2}+p}$的值为（ ）
| A． | p | B． | -p | C． | -$\frac{1}{p}$ | D． | $\frac{1}{p}$ |
14．在给出的以下四个函数中为减函数的是（ ）
| A． | y=2x-5 | B． | y=（x-1）2+3，x∈（1，+∞） | C． | y=$\frac{6}{x}$，x∈（1，+∞） | D． | y=-x2+4x，x∈（-∞，0） |
1．已知△ABC的外接圆半径为R，c=$\sqrt{2}$，且2R（sin2A-sin2C）=（$\sqrt{2}$a-b）sinB（其中a，b分别为A，B的对边），那么R等于（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 4 |
19．
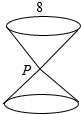如图，某计时沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8，用一个平行于圆锥沙漏的轴的平面α截圆锥，得到的截口曲线为双曲线的一部分，且圆锥顶点P到平面α的距离为2，则此双曲线的离心率为（ ）
如图，某计时沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8，用一个平行于圆锥沙漏的轴的平面α截圆锥，得到的截口曲线为双曲线的一部分，且圆锥顶点P到平面α的距离为2，则此双曲线的离心率为（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |