题目内容
16.如图为函数f(x)=Asin(ωx+φ)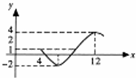 +c(A>0,ω>0,φ>0)图象的一部分.
+c(A>0,ω>0,φ>0)图象的一部分.(Ⅰ)求此函数的周期及最大值和最小值;
(Ⅱ)求此函数的单调递增区间.
分析 (Ⅰ)由函数的最值求出A和c的值,由周期求出ω,可得函数的解析式,进而求得此函数的周期及最大值和最小值.
(Ⅱ)把点(4,1)代入上式求得φ的值,再利用正弦函数的单调性求得f(x)的单调递增区间.
解答 解:(Ⅰ)结合图象及解析表达式可知,c=1,A=4-1=3.
再根据$\frac{3}{4}$•$\frac{2π}{ω}$=12-4,求得ω=$\frac{3π}{16}$,故函数f(x)=3sin($\frac{3π}{16}$x+φ)+1.
故函数f(x)的最小正周期为$\frac{2π}{\frac{3π}{16}}$=$\frac{32}{3}$,最大值为 3+1=4,最小值为-3+1=-2.
(Ⅱ)把点(4,1)代入上式,可得 sin($\frac{3π}{4}$+φ)=0,再根据φ>0,故可取φ=$\frac{π}{4}$,
故函数的解析式为:f(x)=3sin($\frac{3π}{16}$x+$\frac{π}{4}$)+1.
由2kπ-$\frac{π}{2}$≤$\frac{3π}{16}$x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈z,求得-4+$\frac{32}{3}$k≤x≤$\frac{4}{3}$+$\frac{32}{3}$k,
即函数f(x)的单调递增区间为:[-4+$\frac{32}{3}$k,$\frac{4}{3}$+$\frac{32}{3}$k],k∈z.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的周期性、最值、以及单调性,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
11.以下判断正确的是( )
| A. | “b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件. | |
| B. | 命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” | |
| C. | 命题“在△ABC中,若A>B则sinA>sinB”的逆命题为假命题. | |
| D. | 函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件. |
1.已知复数z=$\frac{2i}{1+i}$,则复数z的共轭复数$\overline{z}$是( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
6.已知cosα=$\frac{3}{5}$,则sin2α+cos2α的值为( )
| A. | $\frac{9}{25}$ | B. | $\frac{18}{25}$ | C. | $\frac{23}{25}$ | D. | $\frac{34}{25}$ |
 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.