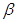题目内容
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC的中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且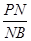 =
=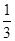 .
.
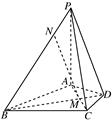
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)设平面PAB∩平面PCD=l,试问直线l是否与直线CD平行,请说明理由.
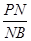 =
=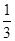 .
.
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)设平面PAB∩平面PCD=l,试问直线l是否与直线CD平行,请说明理由.
(1)见解析(2)见解析(3)不平行
(1)因为△ABC是正三角形,M是AC的中点,
所以BM⊥AC,即BD⊥AC.
又因为PA⊥平面ABCD,BD?平面ABCD,所以PA⊥BD.
又PA∩AC=A,所以BD⊥平面PAC,
又PC?平面PAC,所以BD⊥PC.
(2)在正三角形ABC中,BM=2 ,
,
在△ACD中,因为M为AC的中点,DM⊥AC,所以AD=CD,∠CDA=120°,所以DM= ,所以BM∶MD=3∶1,
,所以BM∶MD=3∶1,
所以BN∶NP=BM∶MD,所以MN∥PD,
又MN?平面PDC,PD?平面PDC,所以MN∥平面PDC.
(3)假设直线l∥CD,因为l?平面PAB,CD?平面PAB,所以CD∥平面PAB.
又CD?平面ABCD,平面PAB∩平面ABCD=AB,
所以CD∥AB.
又知CD与AB不平行,
所以直线l与直线CD不平行.
所以BM⊥AC,即BD⊥AC.
又因为PA⊥平面ABCD,BD?平面ABCD,所以PA⊥BD.
又PA∩AC=A,所以BD⊥平面PAC,
又PC?平面PAC,所以BD⊥PC.
(2)在正三角形ABC中,BM=2
 ,
,在△ACD中,因为M为AC的中点,DM⊥AC,所以AD=CD,∠CDA=120°,所以DM=
 ,所以BM∶MD=3∶1,
,所以BM∶MD=3∶1,所以BN∶NP=BM∶MD,所以MN∥PD,
又MN?平面PDC,PD?平面PDC,所以MN∥平面PDC.
(3)假设直线l∥CD,因为l?平面PAB,CD?平面PAB,所以CD∥平面PAB.
又CD?平面ABCD,平面PAB∩平面ABCD=AB,
所以CD∥AB.
又知CD与AB不平行,
所以直线l与直线CD不平行.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
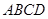 为平行四边形,
为平行四边形,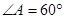 ,
,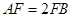 ,
,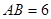 ,点
,点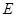 在
在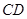 上,
上,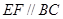 ,
,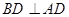 ,
,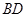 与
与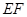 相交于
相交于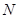 .现将四边形
.现将四边形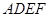 沿
沿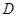 在平面
在平面 上的射影恰在直线
上的射影恰在直线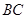 上.
上.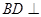 平面
平面 与平面
与平面

 //平面
//平面 ,直线
,直线 平面
平面
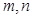 是不同的直线,
是不同的直线,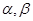 是不同的平面,下列命题中正确的是( )
是不同的平面,下列命题中正确的是( )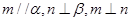 ,则
,则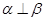
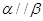
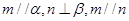 ,则
,则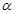 ⊥
⊥