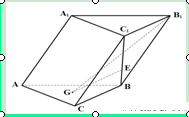
题目内容
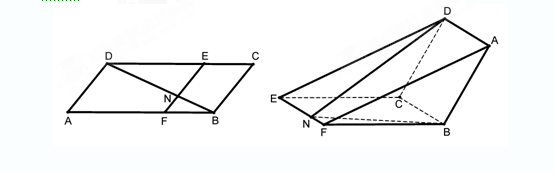
如图,已知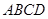 为平行四边形,
为平行四边形,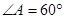 ,
,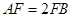 ,
,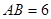 ,点
,点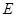 在
在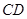 上,
上,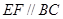 ,
,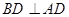 ,
,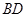 与
与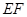 相交于
相交于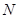 .现将四边形
.现将四边形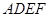 沿
沿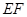 折起,使点
折起,使点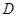 在平面
在平面 上的射影恰在直线
上的射影恰在直线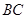 上.
上.
(1)求证: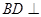 平面
平面 ;
;
(2)求折后直线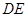 与平面
与平面 所成角的余弦值.
所成角的余弦值.
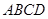 为平行四边形,
为平行四边形,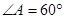 ,
,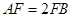 ,
,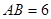 ,点
,点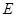 在
在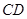 上,
上,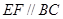 ,
,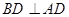 ,
,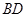 与
与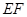 相交于
相交于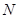 .现将四边形
.现将四边形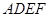 沿
沿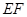 折起,使点
折起,使点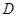 在平面
在平面 上的射影恰在直线
上的射影恰在直线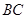 上.
上.(1)求证:
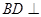 平面
平面 ;
;(2)求折后直线
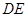 与平面
与平面 所成角的余弦值.
所成角的余弦值.
(1)(2)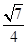
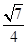
试题分析:(1)连接
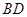 ,欲证
,欲证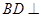 平面
平面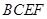 ,只要证点
,只要证点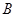 是点
是点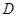 在平面
在平面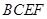 内的射影,易证在平面图中,
内的射影,易证在平面图中,有
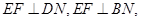 此结论在折后的空间几何体中仍成立
此结论在折后的空间几何体中仍成立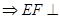 平面
平面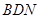
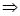 平面
平面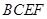
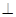 平面
平面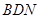
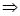 点
点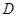 在平面
在平面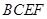 内的射影在直线
内的射影在直线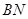 上,结合已知条件,知点
上,结合已知条件,知点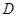 在平面
在平面 上的射影又恰在直线
上的射影又恰在直线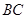 上
上
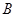 是点
是点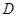 在平面
在平面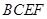 内的射影,从而结论得证.利用勾股定理求出相关线段的长度即可在直角三角形
内的射影,从而结论得证.利用勾股定理求出相关线段的长度即可在直角三角形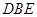 求出
求出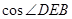 的值.
的值.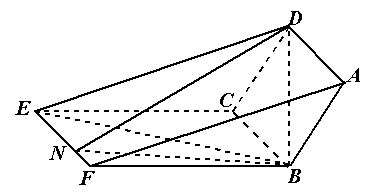
(2)连接
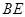 ,由(1)知,
,由(1)知,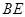 是
是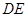 在平面
在平面 内的射影,
内的射影,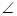
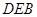 就是所求的线面角,
就是所求的线面角,试题解析:(1)由
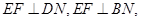 得
得 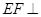 平面
平面 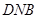
则平面
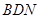
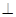 平面
平面 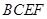
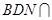 平面
平面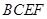
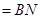
则
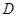 在平面
在平面 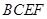 上的射影在直线
上的射影在直线 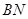 上,
上, 又
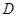 在平面
在平面 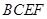 上的射影在直线
上的射影在直线 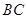 上,
上, 则
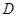 在平面
在平面 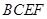 上的射影即为点
上的射影即为点 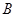 ,
, 故
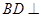 平面
平面 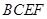
(2)连接
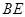 ,由
,由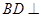 平面
平面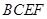 ,得
,得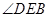 即为直线
即为直线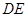 与平面
与平面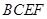 所成的角,
所成的角,在原图中,由已知,可得
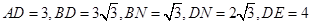
折后,由
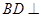 平面
平面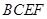 ,知
,知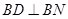
则
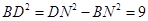 ,即
,即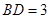
则在
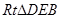 中,有
中,有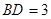 ,
,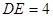 ,则
,则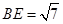 ,
,故
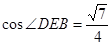
即折后直线
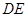 与平面
与平面 所成角的余弦值为
所成角的余弦值为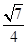 . 12分
. 12分
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 中,侧面
中,侧面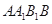 ⊥底面
⊥底面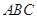 ,侧棱
,侧棱 与底面
与底面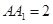 .底面
.底面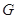 点,
点,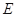 是线段
是线段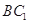 上一点,且
上一点,且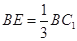 .
.
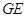 //侧面
//侧面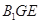 与底面
与底面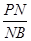 =
=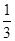 .
.
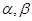 表示平面,m,n表示直线,
表示平面,m,n表示直线, 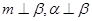 ,给出下列四个结论:
,给出下列四个结论: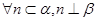 ;②
;②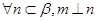 ;③
;③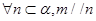 ;④
;④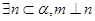 ,
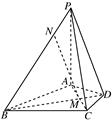
,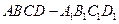 的棱长为a,M、N分别为
的棱长为a,M、N分别为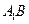 和AC上的点,
和AC上的点,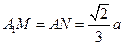 ,则MN与平面
,则MN与平面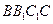 的位置关系是( )
的位置关系是( )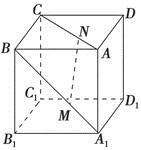
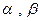 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
,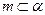 ,
, ,则
,则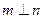
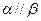 ,
,
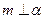 ,
,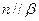 ,则
,则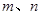 是两条不同的直线,
是两条不同的直线, 是两个不同的平面。下列四个命题正确的是( )
是两个不同的平面。下列四个命题正确的是( )


