题目内容
16.已知函数f(x)是定义在R上的奇函数,且满足f(-1-x)=f(3+x).当x∈(0,1]时,f(x)=2x-1.(1)当x∈[1,2]时,求函数解析式;
(2)求f(0)+f(1)+f(2)+f(3)+…+f(2013)的值.
分析 (1)由已知中定义在R上的函数y=f(x)是奇函数,且满足f(-1-x)=f(3+x),求出函数的对称轴和对称中心,根据函数对称性与周期性之间的关系,求出函数的周期,
(2)求出函数一个周期内的数值的和,然后求解函数值即可.
解答 解:(1)∵函数f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),f(0)=0,
∵f(-1-x)=f(3+x).
∴函数关于x=1对称,
所以函数的周期为4.
可得f(x-1)=f(3-x),可得f(x)=f(2-x),
当x∈[1,2]时,2-x∈[0,1].
f(x)=2(2-x)-1=3-2x.
(2)f(0)+f(1)+f(2)+f(3)=-1+1-1+f(-1)=-1-f(1)=-2.
f(0)+f(1)+f(2)+f(3)+…+f(2013)=503×[f(0)+f(1)+f(2)+f(3)]+f(0)+f(1)
=-1006.
点评 本题综合考查了抽象函数的应用,函数的性质周期性运奇偶性的运用,整体运用的思想,考查了逻辑推理变换的能力,属于中档题.

练习册系列答案
相关题目
11.已知抛物线y2=8x焦点与双曲线$\frac{x^2}{a^2}-{y^2}=1$(a>0)的右焦点重合,则此双曲线的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
1.设函数f(x)=2x,则如图所示的函数图象( )
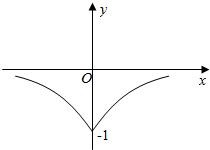

| A. | y=f(|x|) | B. | y=-|f(x)| | C. | y=-f(-|x|) | D. | y=f(-|x|) |
8.设[m]表示不超过实数m的最大整数,则在直角坐标平面xOy上满足[x]2+4[y]2=100的点P(x,y)所形成的图形的面积为( )
| A. | 10 | B. | 12 | C. | 10π | D. | 12π |
5.已知函数f(x)=Asin(ωx+φ)(A≠0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)关于直线x=$\frac{2π}{3}$对称,且它的最小正周期为π,则( )
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | ||
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | D. | f(x)的图象的一条对称轴是x=$\frac{5π}{12}$ |