题目内容

4．已知f（x）=$\sqrt{（1-{a}^{2}）{x}^{2}}$+3（1-a）x+b，f（x）定义域为R，求a的范围．

分析 把f（x）定义域为R转化为（1-a2）x2≥0对任意实数x恒成立，即1-a2≥0，解不等式求得a的取值范围．

解答 解：∵f（x）=$\sqrt{（1-{a}^{2}）{x}^{2}}$+3（1-a）x+b的定义域为R，
∴（1-a2）x2≥0对任意实数x恒成立，
则1-a2≥0，即-1≤a≤1．
∴实数a的范围是[-1，1]．

点评 本题考查函数定义域的求法，考查了数学转化思想方法，是基础题．

练习册系列答案
相关题目
10．函数y=-$\frac{2}{x}$+1在[1，3]上的最大值为$\frac{1}{3}$最小值为-1．
15．证明函数f（x）=$\frac{2}{x}$在（0，+∞）上是减函数．
12．已知等差数列{an}的前n项和Sn，满足a2013=S2013=2013，则a1=（　　）
A．-2014B．-2013C．-2012D．-2011
19．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1（a＞$\sqrt{2}$）的两条渐近线的夹角为$\frac{π}{3}$，则双曲线的离心率为（　　）
A．$\frac{2\sqrt{3}}{3}$B．$\frac{2\sqrt{6}}{3}$C．$\sqrt{3}$D．2
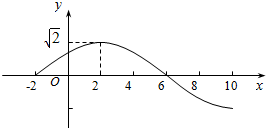9．已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜$\frac{π}{2}$）的部分图象如图所示．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）在△ABC中，内角A，B，C的对边分别为a，b，c，若f（x）在x∈[4，12]上的最大值为c，且C=$\frac{π}{3}$．求△ABC的面积的最大值．
16．已知函数f（x）是定义在R上的奇函数，且满足f（-1-x）=f（3+x）．当x∈（0，1]时，f（x）=2x-1．
（1）当x∈[1，2]时，求函数解析式；
（2）求f（0）+f（1）+f（2）+f（3）+…+f（2013）的值．
13．已知数列{an}满足：a1=$\frac{1}{2}$，$\frac{1}{{{a_{n+1}}}}=\frac{1}{{a_n^2+{a_n}}}$用[x]表示不超过x的最大整数，则$[\frac{1}{{{a_1}+1}}+\frac{1}{{{a_2}+1}}+…+\frac{1}{{{a_{2015}}+1}}]$的值等于（　　）
A．0B．1C．2D．3
14．若函数f（x）=alog2$\frac{x}{8}$•log2（4x）在区间[$\frac{1}{8}$，4]上的最大值是25，求实数a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网