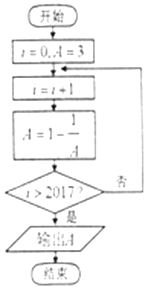
题目内容
【题目】如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE= ![]() ,∠EAD=∠EAB.
,∠EAD=∠EAB. 
(1)证明:平面ACEF⊥平面ABCD;
(2)若AE与平面ABCD所成角为60°,求二面角B﹣EF﹣D的余弦值.
【答案】
(1)证明:连接EG,
∵四边形ABCD为菱形,∴AD=AB,BD⊥AC,DG=GB,
在△EAD和△EAB中,
AD=AB,AE=AE,∠EAD=∠EAB,
∴△EAD≌△EAB,
∴ED=EB,则BD⊥EG,
又AC∩EG=G,∴BD⊥平面ACEF,
∵BD平面ABCD,
∴平面ACEF⊥平面ABCD
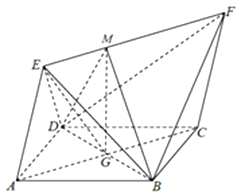
(2)解法一:过G作EF的垂线,垂足为M,连接MB,MG,MD,
易得∠EAC为AE与面ABCD所成的角,
∴∠EAC=60°,
∵EF⊥GM,EF⊥BD,
∴EF⊥平面BDM,
∴∠DMB为二面角B﹣EF﹣D的平面角,
可求得MG= ![]() ,DM=BM=
,DM=BM= ![]() ,
,
在△DMB中,由余弦定理可得:cos∠BMD= ![]() ,
,
∴二面角B﹣EF﹣D的余弦值为 ![]() ;
;
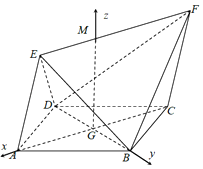
解法二:如图,在平面ABCD内,过G作AC的垂线,交EF于M点,
由(1)可知,平面ACEF⊥平面ABCD,
∵MG⊥平面ABCD,
∴直线GM、GA、GB两两互相垂直,
分别以GA、GB、GM为x、y、z轴建立空间直角坐标系G﹣xyz,
可得∠EAC为AE与平面ABCD所成的角,∴∠EAC=60°,
则D(0,﹣1,0),B(0,1,0),E( ![]() ),F(
),F( ![]() ),
),
![]() ,
, ![]() ,
,
设平面BEF的一个法向量为 ![]() ,则
,则
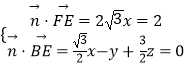 ,
,
取z=2,可得平面BEF的一个法向量为 ![]() ,
,
同理可求得平面DEF的一个法向量为 ![]() ,
,
∴cos< ![]() >=
>= ![]() =
= ![]() ,
,
∴二面角B﹣EF﹣D的余弦值为 ![]() .
.
【解析】(1)连接EG,由四边形ABCD为菱形,可得AD=AB,BD⊥AC,DG=GB,可证△EAD≌△EAB,进一步证明BD⊥平面ACEF,则平面ACEF⊥平面ABCD;(2)法一、过G作EF的垂线,垂足为M,连接MB,MG,MD,可得∠EAC为AE与面ABCD所成的角,得到EF⊥平面BDM,可得∠DMB为二面角B﹣EF﹣D的平面角,在△DMB中,由余弦定理求得∠BMD的余弦值,进一步得到二面角B﹣EF﹣D的余弦值;法二、在平面ABCD内,过G作AC的垂线,交EF于M点,由(1)可知,平面ACEF⊥平面ABCD,得MG⊥平面ABCD,则直线GM、GA、GB两两互相垂直,分别以GA、GB、GM为x、y、z轴建立空间直角坐标系G﹣xyz,分别求出平面BEF与平面DEF的一个法向量,由两法向量所成角的余弦值可得二面角B﹣EF﹣D的余弦值.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.