题目内容
【题目】定义在R上的函数f(x),当x∈[0,2]时,f(x)=4(1﹣|x﹣1|),且对于任意实数x∈[2n﹣2,2n+1﹣2](n∈N* , n≥2),都有f(x)= ![]() f(
f( ![]() ﹣1).若g(x)=f(x)﹣logax有且只有三个零点,则a的取值范围是( )
﹣1).若g(x)=f(x)﹣logax有且只有三个零点,则a的取值范围是( )
A.[2,10]
B.[ ![]() ,
, ![]() ]
]
C.(2,10)
D.[2,10)
【答案】C
【解析】解:当x∈[0,2]时,f(x)=4(1﹣|x﹣1|), 当n=2时,x∈[2,6],此时 ![]() ﹣1∈[0,2],则f(x)=
﹣1∈[0,2],则f(x)= ![]() f(
f( ![]() ﹣1)=
﹣1)= ![]() ×4(1﹣|
×4(1﹣| ![]() ﹣1﹣1|)=2(1﹣|
﹣1﹣1|)=2(1﹣| ![]() ﹣2|),
﹣2|),
当n=3时,x∈[6,14],此时 ![]() ﹣1∈[2,6],则f(x)=
﹣1∈[2,6],则f(x)= ![]() f(
f( ![]() ﹣1)=
﹣1)= ![]() ×2(1﹣|
×2(1﹣| ![]() ﹣
﹣ ![]() |)=1﹣|
|)=1﹣| ![]() ﹣
﹣ ![]() |,
|,
由g(x)=f(x)﹣logax=0,得f(x)=logax,分别作出函数f(x)和y=logax的图象,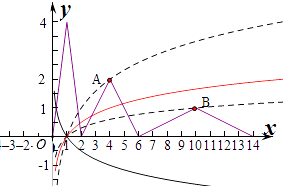
若0<a<1,则此时两个函数图象只有1个交点,不满足条件.
若a>1,当对数函数图象经过A时,两个图象只有2个交点,当图象经过点B时,两个函数有4个交点,
则要使两个函数有3个交点,则对数函数图象必须在A点以下,B点以上,
∵f(4)=2,f(10)=1,∴A(4,2),B(10,1),
即满足 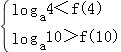 ,
,
即 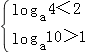 ,解得
,解得 ![]() ,
,
即2<a<10,
故选:C.

练习册系列答案
相关题目

