题目内容
抛物线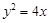 的焦点为
的焦点为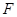 ,点
,点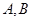 在抛物线上,且
在抛物线上,且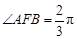 ,弦
,弦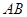 中点
中点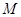 在准线
在准线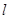 上的射影为
上的射影为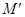 ,则
,则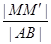 的最大值为( )
的最大值为( )
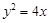 的焦点为
的焦点为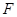 ,点
,点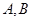 在抛物线上,且
在抛物线上,且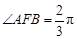 ,弦
,弦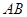 中点
中点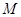 在准线
在准线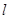 上的射影为
上的射影为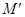 ,则
,则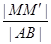 的最大值为( )
的最大值为( )A.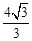 | B.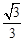 | C.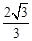 | D.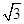 |
B
试题分析:如图,
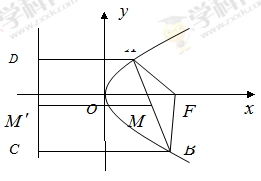
过点
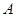 作
作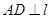 于
于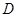 ,
,过点
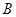 作
作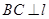 于
于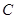 ,
,在
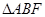 中,由余弦定理,
中,由余弦定理, 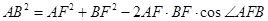 ,
,∴
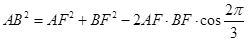 ,
,即
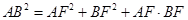 ,由抛物线的定义,有
,由抛物线的定义,有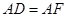 ,
,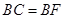 ,
,∴
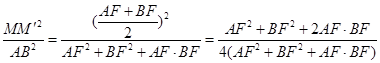
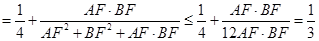 ,
,∴
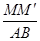 的最大值为
的最大值为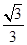 ,当且仅当
,当且仅当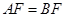 取得最大值.
取得最大值.
练习册系列答案
相关题目
题目内容
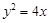 的焦点为
的焦点为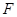 ,点
,点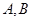 在抛物线上,且
在抛物线上,且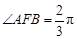 ,弦
,弦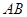 中点
中点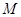 在准线
在准线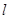 上的射影为
上的射影为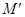 ,则
,则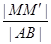 的最大值为( )
的最大值为( )A.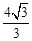 | B.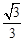 | C.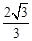 | D.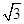 |

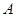 作
作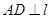 于
于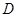 ,
,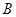 作
作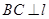 于
于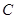 ,
,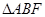 中,由余弦定理,
中,由余弦定理, 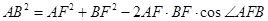 ,
,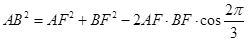 ,
,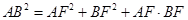 ,由抛物线的定义,有
,由抛物线的定义,有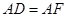 ,
,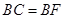 ,
,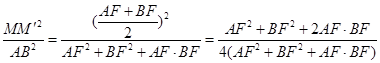
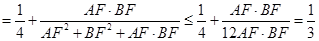 ,
,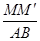 的最大值为
的最大值为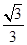 ,当且仅当
,当且仅当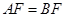 取得最大值.
取得最大值.