题目内容
(本小题满分15分) 已知函数
已知函数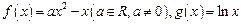 .
.
(Ⅰ)当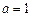 时,判断函数
时,判断函数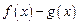 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数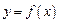 与
与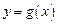 的图象有两个不同的交点
的图象有两个不同的交点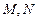 ,求
,求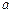 的取值范围;
的取值范围;
(Ⅲ)设点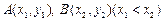 是函数
是函数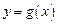 图象上的两点,平行于
图象上的两点,平行于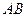 的切线以
的切线以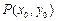 为切点,求证:
为切点,求证: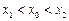 .
.
 已知函数
已知函数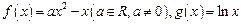 .
.(Ⅰ)当
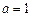 时,判断函数
时,判断函数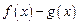 在定义域上的单调性;
在定义域上的单调性;(Ⅱ)若函数
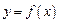 与
与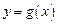 的图象有两个不同的交点
的图象有两个不同的交点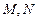 ,求
,求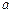 的取值范围;
的取值范围;(Ⅲ)设点
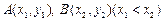 是函数
是函数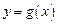 图象上的两点,平行于
图象上的两点,平行于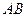 的切线以
的切线以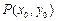 为切点,求证:
为切点,求证: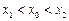 .
.(Ⅰ)(0,1)上单调递减,在 上单调递增 (Ⅱ)
上单调递增 (Ⅱ)  (Ⅲ)见解析
(Ⅲ)见解析
 上单调递增 (Ⅱ)
上单调递增 (Ⅱ)  (Ⅲ)见解析
(Ⅲ)见解析(Ⅰ)记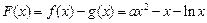 ,则
,则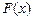 的定义域为
的定义域为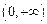 .
.
当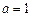 时,因
时,因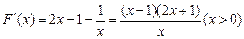 ,
,
所以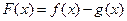 在(0,1)上单调递减,在
在(0,1)上单调递减,在 上单调递增.……4分
上单调递增.……4分
(Ⅱ)由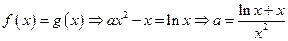
 .
.
令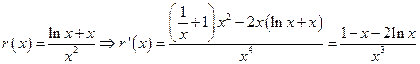 .
.
当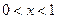 时,
时,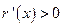 ,
, 则
则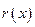 单调递增,且
单调递增,且 ;
;
当 时,
时,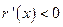 ,则
,则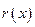 单调递减,且
单调递减,且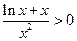 .
.
所以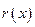 在
在 处取到最大值
处取到最大值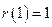 .
.
所以要使 与
与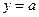 有两个不同的交点,只需
有两个不同的交点,只需 .…………9分
.…………9分
(III)由已知: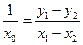 ,所以
,所以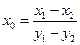 .
.
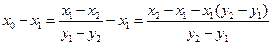 =
=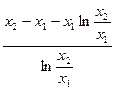 .
.
设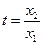 得:
得: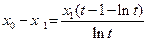
 .
.
构造函数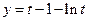 ,当
,当 时,
时, ,
,
所以函数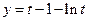 在当
在当 时是增函数.
时是增函数.
于是 ,
,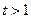 时,
时, ,则
,则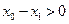 ,得
,得 成立.
成立.
同理,可证得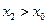 成立,从而求证成立.……………………15分
成立,从而求证成立.……………………15分
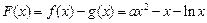 ,则
,则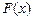 的定义域为
的定义域为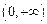 .
.当
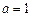 时,因
时,因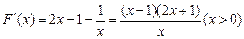 ,
,所以
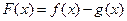 在(0,1)上单调递减,在
在(0,1)上单调递减,在 上单调递增.……4分
上单调递增.……4分(Ⅱ)由
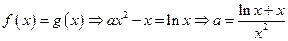
 .
.令
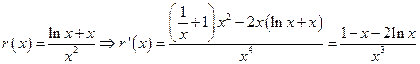 .
.当
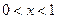 时,
时,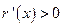 ,
, 则
则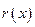 单调递增,且
单调递增,且 ;
;
当
 时,
时,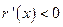 ,则
,则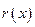 单调递减,且
单调递减,且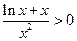 .
.所以
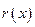 在
在 处取到最大值
处取到最大值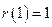 .
.所以要使
 与
与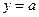 有两个不同的交点,只需
有两个不同的交点,只需 .…………9分
.…………9分(III)由已知:
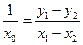 ,所以
,所以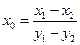 .
.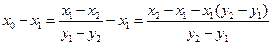 =
=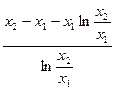 .
.设
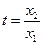 得:
得: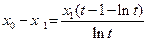
 .
.构造函数
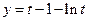 ,当
,当 时,
时, ,
,所以函数
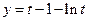 在当
在当 时是增函数.
时是增函数.于是
 ,
,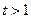 时,
时, ,则
,则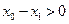 ,得
,得 成立.
成立.同理,可证得
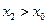 成立,从而求证成立.……………………15分
成立,从而求证成立.……………………15分
练习册系列答案
相关题目
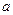 ,在今后
,在今后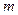 年内,计划使产量平均每年比上一年增加
年内,计划使产量平均每年比上一年增加 ,写出产量随年数变化的函数解析式.
,写出产量随年数变化的函数解析式. ,例如:1
,例如:1 2=1,3
2=1,3 的值域为 .
的值域为 . 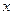 表示床价,用
表示床价,用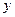 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入) ,若初时含杂质
,若初时含杂质 ,每过滤一次可使杂质含量减少
,每过滤一次可使杂质含量减少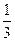 ,问至少应过滤几次才能使产品达到市场要求?(已知
,问至少应过滤几次才能使产品达到市场要求?(已知 )
) 包.已知每次进货运输劳务费为62.5元,全年保管费为
包.已知每次进货运输劳务费为62.5元,全年保管费为 元.求:
元.求: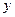 元表示为每次进货量
元表示为每次进货量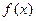 是奇函数,
是奇函数,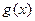 是偶函数,并且
是偶函数,并且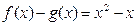 ,求
,求