题目内容
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)判断![]() 的奇偶性并证明;
的奇偶性并证明;
(2)若![]() ,是否存在
,是否存在![]() ,使
,使![]() 在
在![]() 的值域为
的值域为![]() ?若存在,求出此时
?若存在,求出此时![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)奇函数;证明见解析;(2)存在,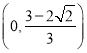 .
.
【解析】
(1)求出函数![]() 的定义域,然后利用奇偶性的定义验证函数
的定义域,然后利用奇偶性的定义验证函数![]() 的奇偶性;
的奇偶性;
(2)由![]() ,可得出
,可得出![]() ,利用复合函数可分析出函数
,利用复合函数可分析出函数![]() 在区间
在区间![]() 上为减函数,由题意得
上为减函数,由题意得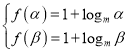 ,于是得出关于
,于是得出关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两解,即关于
上有两解,即关于![]() 的方程
的方程![]() 在
在![]() 上有两个不等的实根,然后结合二次函数的图象列出关于
上有两个不等的实根,然后结合二次函数的图象列出关于![]() 的不等式组,解出即可.
的不等式组,解出即可.
(1)函数![]() 是奇函数;证明如下:
是奇函数;证明如下:
由![]() 解得
解得![]() 或
或![]() ,所以,函数
,所以,函数![]() 的定义域为
的定义域为![]() ,关于原点对称.
,关于原点对称.
![]() ,
,
因此,函数![]() 为奇函数;
为奇函数;
(2)由题意知,![]() ,且
,且![]() ,
,![]() .
.
令![]() 在
在![]() 上为增函数,
上为增函数,
而函数![]() 为减函数,所以,函数
为减函数,所以,函数![]() 在
在![]() 上为减函数,
上为减函数,
假设存在![]() ,使得题意成立,则函数
,使得题意成立,则函数![]() 在
在![]() 上为减函数,
上为减函数,
则有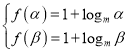 ,即
,即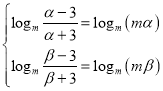 ,
,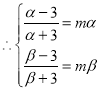 .
.
所以![]() 、
、![]() 是方程
是方程![]() 的两正根,
的两正根,
整理得![]() 在
在![]() 有
有![]() 个不等根
个不等根![]() 和
和![]() ,由韦达定理得
,由韦达定理得![]() ,则
,则![]() .
.
令![]() ,则函数
,则函数![]() 在
在![]() 有
有![]() 个零点,
个零点,
则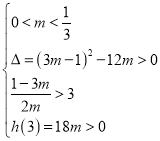 ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是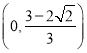 .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
