题目内容
【题目】已知函数
．
（1）求函数f（x）在[0，π]上的单调递减区间；
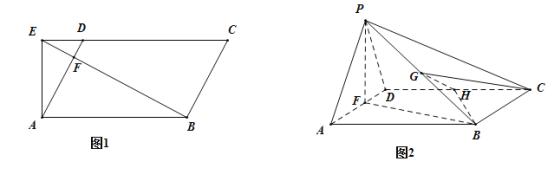
（2）在锐角△ABC的内角A，B，C所对边为a，b，c，已知f（A）＝﹣1，a＝2，求△ABC的面积的最大值．
【答案】（1）单调递减区间为
和
．（2）
．
【解析】
（1）先把函数f（x）化简成
．再利用正弦函数的单调性求单调区间．
（2）把f（A）＝﹣1代入函数解析式求出A，再有余弦定理列出b，c的方程，利用均值不等式求出bc的最大值，进而求△ABC的面积的最大值．
解：（1）
∴
，∴
（k∈Z）
∴函数f（x）在[0，π]的单调递减区间为
和．
（2）∵△ABC为锐角三角形，∴
，
又
，即
．
∵a2＝b2+c2﹣2bcosA＝b2+c2﹣bc≥2bc﹣bc＝bc，又a＝2，∴bc≤4，
∴
．当且仅当b＝c＝2时，△ABC的面积取得最大值
．
练习册系列答案
相关题目
【题目】新生儿某疾病要接种三次疫苗免疫（即0、1、6月龄），假设每次接种之间互不影响，每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系，现进行了两种接种方案的临床试验：10μg/次剂量组与20μg/次剂量组，试验结果如下：
接种成功 | 接种不成功 | 总计（人） | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计（人） | 1873 | 127 | 2000 |
（1）根据数据说明哪种方案接种效果好？并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关？
（2）以频率代替概率，若选用接种效果好的方案，参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式：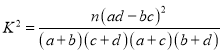
，其中
参考附表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
