题目内容
【题目】设函数![]() ,
,
(1)当![]() 时,求函数
时,求函数![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)求![]() 的单调区间;
的单调区间;
(3)若不等式![]() 对
对![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)单调递增区间是
;(2)单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(3)2
;(3)2
【解析】
(1)当![]() 时,可得
时,可得![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,即可求出切线方程;
,即可求出切线方程;
(2)求出![]() ,求出极值点,利用导函数的符号,判断函数的单调性即可;
,求出极值点,利用导函数的符号,判断函数的单调性即可;
(3)当![]() 时,不等式
时,不等式![]() 恒成立,即:
恒成立,即:![]() 恒成立,等价于当
恒成立,等价于当![]() 时,
时,![]() 恒成立;即
恒成立;即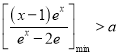 对
对![]() 恒成立,令
恒成立,令![]() ,根据导数求其最值,即可求得答案.
,根据导数求其最值,即可求得答案.
(1)当![]() 时,
时,
可得![]() ,
,
![]()
![]() ,
,
可得:![]() ,
,![]()
![]() 所求切线方程为
所求切线方程为![]()
(2)![]()
![]()
![]()
![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
![]()
![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(3)当![]() 时,不等式
时,不等式![]() 恒成立
恒成立
即:![]() 恒成立,
恒成立,
等价于当![]() 时,
时,![]() 恒成立;
恒成立;
即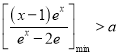 对
对![]() 恒成立.
恒成立.
令![]() ,
,![]() ,
,
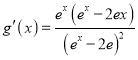 ,
,
令![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() 在
在![]() 上单调递增.
上单调递增.
又![]()
![]() ,
,![]() ,
,
![]()
![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,且
,且![]() ,
,![]()
![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]()
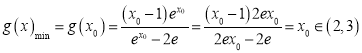 ,
,
![]()
![]() ,
,
故整数![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:cm)落在各个小组的频数分布如下表:
数据分组 | [12.5,15.5) | [15.5,18.5) | [18.5,21.5) | [21.5,24.5) | [24.5,27.5) | [27.5,30.5) | [30.5,33.5) |
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在[27.5,33.5]内的概率;
(2)求这50件产品尺寸的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() (
(![]() ).
).
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]() ;(2)
;(2)![]() .
.