题目内容
曲线y2=4x关于直线x=2对称的曲线方程是( )
| A.y2=8-4x | B.y2=4x-8 |
| C.y2=16-4x | D.y2=4x-16 |
C
要求曲线y2=4x关于直线x=2对称的曲线方程,我们可采用坐标法,即设出待求曲线上任一点为P(x,y),然后根据P点关于直线x=2对称的Q(4-x,y)在曲线y2=4x上,然后将Q点代入曲线y2=4x中,即可得到x,y之间的关系,即为所求曲线的方程.
解:设曲线y2=4x关于直线x=2对称的曲线为C,
在曲线C上任取一点P(x,y),
则P(x,y)关于直线x=2的对称点为Q(4-x,y).
因为Q(4-x,y)在曲线y2=4x上,
所以y2=4(4-x),
即y2=16-4x.
故选C.
解:设曲线y2=4x关于直线x=2对称的曲线为C,
在曲线C上任取一点P(x,y),
则P(x,y)关于直线x=2的对称点为Q(4-x,y).
因为Q(4-x,y)在曲线y2=4x上,
所以y2=4(4-x),
即y2=16-4x.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
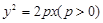 上横坐标是5的点
上横坐标是5的点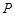 到其焦点
到其焦点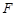 的距离是8,则以
的距离是8,则以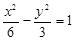 的渐近线相切的圆的方程是
的渐近线相切的圆的方程是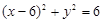
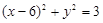
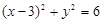
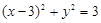
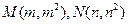 是抛物线
是抛物线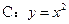 上两个不同点,且
上两个不同点,且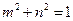 ,
,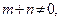 直线
直线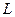 是线段
是线段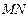 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为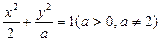 .
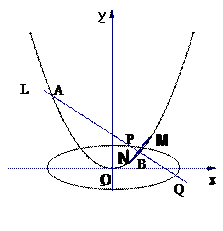
.
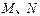 在
在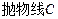 上移动时,求直线
上移动时,求直线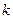 的取值范围;
的取值范围;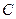 交于A、B两个不同点,
交于A、B两个不同点, 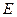 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为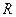 ,
,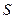 ,若
,若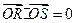 ,求
,求 为F,准线为L,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥L,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是
为F,准线为L,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥L,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 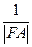 +
+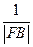 为定值.
为定值. 在交点处的切线方程。
在交点处的切线方程。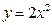 的准线方程为
的准线方程为 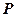 为抛物线
为抛物线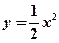 上的动点,点
上的动点,点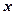 轴上的射影为
轴上的射影为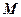 ,点
,点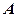 的坐标是
的坐标是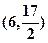 ,则
,则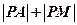 的最小值是 ( )
的最小值是 ( )