题目内容
直线l过抛物线C∶y2=2px(p>0)的焦点F,且交抛物线C于A,B两点,分别从A,B两点向抛物线的准线引垂线,垂足分别为A1,B1,则∠A1FB1是
( )
( )
| A.锐角 | B.直角 |
| C.钝角 | D.直角或钝角 |
B
先由抛物线定义可知AA1=AF,可推断∠1=∠2;又根据AA1∥x轴,可知∠1=∠3,进而可得∠2=∠3,同理可求得∠4=∠6,最后根据
∴∠A1FB1=∠3+∠6答案可得.
解:如图,由抛物线定义可知AA1=AF,故∠1=∠2,
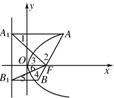
又∵AA1∥x轴,
∴∠1=∠3,从而∠2=∠3,同理可证得∠4=∠6,
∴∠A1FB1=∠3+∠6=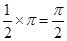 ,
,
故选B
∴∠A1FB1=∠3+∠6答案可得.
解:如图,由抛物线定义可知AA1=AF,故∠1=∠2,

又∵AA1∥x轴,
∴∠1=∠3,从而∠2=∠3,同理可证得∠4=∠6,
∴∠A1FB1=∠3+∠6=
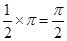 ,
,故选B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
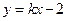 与抛物线C:
与抛物线C: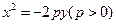 交于A,B两点,
交于A,B两点,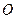 为坐标原点,
为坐标原点,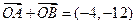 。
。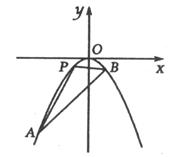
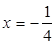 为准线的抛物线的标准方程为 ( )
为准线的抛物线的标准方程为 ( )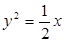
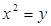
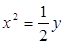
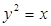
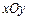 中的抛物线
中的抛物线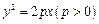 的焦点
的焦点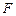 作一条倾斜角为
作一条倾斜角为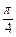 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.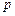 表示A、B之间的距离;
表示A、B之间的距离;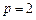 时,求
时,求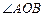 的余弦值.
的余弦值.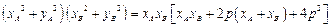 .
.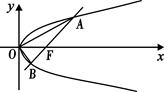
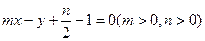 经过抛物线
经过抛物线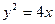 的焦点,则
的焦点,则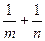 的
的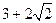
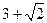
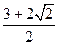
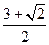
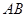 是过抛物线
是过抛物线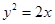 焦点的弦,
焦点的弦,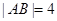 ,则
,则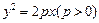 的焦点作倾斜角为
的焦点作倾斜角为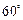 的直线,与抛物线分别交于
的直线,与抛物线分别交于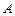 ,
,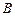 两点(点
两点(点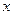 轴上方),
轴上方),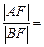
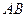 ⊥
⊥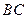 ,
,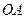 ∥
∥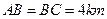 ,
,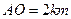 ,
, 曲线段
曲线段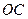 是以点
是以点 为顶
为顶 点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落
点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落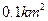 ).
).