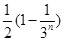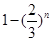题目内容
在数列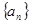 中,如果存在常数
中,如果存在常数
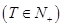 ,使得
,使得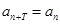 对于任意正整数
对于任意正整数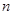 均成立,那么就称数列
均成立,那么就称数列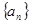 为周期数列,其中
为周期数列,其中 叫做数列
叫做数列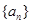 的周期. 已知数列
的周期. 已知数列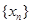 满足
满足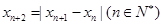 ,若
,若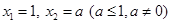 ,当数列
,当数列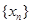 的周期为
的周期为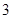 时,则数列
时,则数列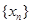 的前2012项的和
的前2012项的和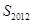 为 ( )
为 ( )
| A.1339 +a | B.1341+a | C.671 +a | D.672+a |
B
解析试题分析:先要弄清题意中所说的周期数列的含义,然后利用这个定义,针对题目中的数列的周期,先求x3,再前三项和s3,最后求s2012.
∵xn+1=|xn-xn-1|(n≥2,n∈N*),且x1=1,x2=a(a≤1,a≠0),∴x3=|x2-x1|=1-a,∴该数列的前3项的和s3=1+a+(1-a)=2∵数列{xn}周期为3,∴该数列的前2012项的和s2012=s2010+x1+x2=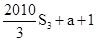 =1341+a,选B.
=1341+a,选B.
考点:本试题主要以周期数列为载体,考查数列具的周期性,考查该数列的前n项和.
点评:解决该试题的关键在于应由题意先求一个周期的和,再求该数列的前n项和sn.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
若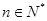 ,则1+2+22+23+…+2n-1=
,则1+2+22+23+…+2n-1=
| A.2n-1-1 | B.2n-1 | C.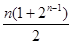 | D.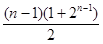 |
已知等比数列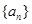 的公比为正数,且
的公比为正数,且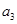
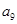 =2
=2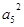 ,
,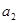 =1,则
=1,则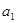 =( )
=( )
A.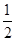 | B.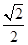 | C.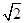 | D.2 |
远望灯塔高七层,红光点点倍加增,只见顶层灯一盏,请问共有几盏灯?答曰:( )
| A.64 | B.128 | C.63 | D.127 |
设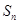 为等比数列
为等比数列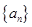 的前
的前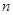 项和,已知
项和,已知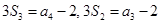 ,则公比
,则公比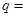 ( )
( )
| A.4 | B.3 | C.2 | D.8 |
在等比数列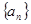 中,
中,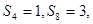 则
则 的值是( )
的值是( )
| A.14 | B.16 | C.18 | D.20 |
设 为等比数列
为等比数列 的前
的前 项和,已知
项和,已知 ,
,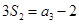 ,则公比
,则公比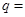 ( )
( )
| A. 3 | B. 4 | C. 5 | D. 6 |
 的首项、公比之和为1且首项是公比的2倍,那么它的前
的首项、公比之和为1且首项是公比的2倍,那么它的前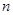 项的和为
项的和为