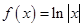题目内容
已知等比数列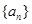 的公比为正数,且
的公比为正数,且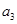
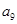 =2
=2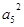 ,
,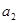 =1,则
=1,则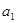 =( )
=( )
A.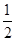 | B.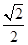 | C.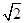 | D.2 |
B
解析试题分析:因为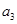
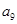 =2
=2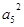 ,所以
,所以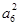 =2
=2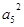 ,即
,即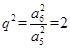 ,又因为
,又因为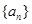 的公比为正数,所以
的公比为正数,所以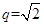 。所以
。所以
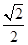 。
。
考点:等比数列的简单性质;等比中项。
点评:灵活应用等比数列的性质是做此题的关键。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列 是等差数列,
是等差数列,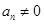 若
若 ,则
,则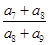 的值是( )
的值是( )
A.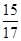 | B.1或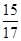 | C.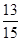 | D.1或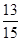 |
公比为2的等比数列{ } 的各项都是正数,且
} 的各项都是正数,且 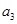
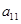 =16,则
=16,则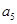 =( )
=( )
| A. 1 | B. 2 | C. 4 | D. 8 |
已知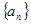 是等比数列,
是等比数列,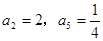 ,则公比
,则公比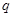 =( )
=( )
A.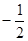 | B.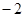 | C.2 | D.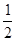 |
设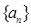 是各项为正数的无穷数列,
是各项为正数的无穷数列,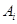 是边长为
是边长为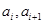 的矩形面积(
的矩形面积(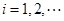 ),则
),则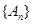 为等比数列的充要条件为
为等比数列的充要条件为
A.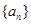 是等比数列。 是等比数列。 |
B.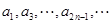 或 或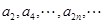 是等比数列。 是等比数列。 |
C.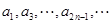 和 和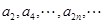 均是等比数列。 均是等比数列。 |
D.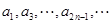 和 和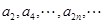 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
设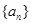 是等比数列,若
是等比数列,若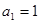 ,
,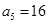 ,则
,则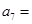 ( )
( )
| A.63 | B.64 | C.127 | D.128 |
在数列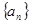 中,如果存在常数
中,如果存在常数
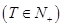 ,使得
,使得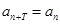 对于任意正整数
对于任意正整数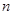 均成立,那么就称数列
均成立,那么就称数列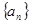 为周期数列,其中
为周期数列,其中 叫做数列
叫做数列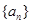 的周期. 已知数列
的周期. 已知数列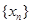 满足
满足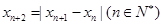 ,若
,若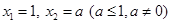 ,当数列
,当数列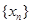 的周期为
的周期为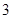 时,则数列
时,则数列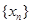 的前2012项的和
的前2012项的和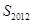 为 ( )
为 ( )
| A.1339 +a | B.1341+a | C.671 +a | D.672+a |
设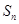 为等比数列
为等比数列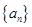 的前
的前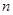 项和,已知
项和,已知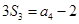 ,
,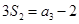 ,则公比
,则公比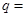 ( )
( )
| A.3 | B.4 | C.5 | D.6 |
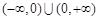 上的函数
上的函数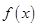 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,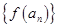 仍是等比数列,则称
仍是等比数列,则称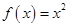 ②
②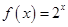 ③
③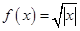 ④
④