题目内容
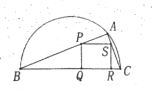
【题目】如图,某市园林局准备绿化一块直径为![]() 的半圆空地,
的半圆空地,![]() 以外的地方种草,
以外的地方种草,![]() 的内接正方形
的内接正方形![]() 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若![]() 为定值),
为定值),![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]()
(1)用![]() 表示
表示![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 取得最大值,并求出此最大值.
取得最大值,并求出此最大值.
【答案】(1) ![]()
![]() ;(2)
;(2) ![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .
.
【解析】试题分析:(1)在Rt△ABC中,BC=a,∠ABC=α,由AB=acosα,AC=asinα,能求出S1;设正方形PQRS的边长为x,则BP=![]() ,AP=xcosα,由BP+AP=
,AP=xcosα,由BP+AP=![]() ,AB=acosα,AP+BP=AB,能求出S2.
,AB=acosα,AP+BP=AB,能求出S2.
(2)![]() =
=![]() ,令sin2α=t,推导出
,令sin2α=t,推导出![]() =
=![]() ,0<t≤1,设f(t)=
,0<t≤1,设f(t)=![]() (0<t≤1),推导出f(t)=
(0<t≤1),推导出f(t)=![]() 在(0,1]上单调递减,由此能求出
在(0,1]上单调递减,由此能求出![]() 的最大值及相应的α.
的最大值及相应的α.
试题解析:
(1)在![]() 中,
中,![]() ,
,
所以![]()
设正方形![]() 的边长为
的边长为![]() ,则
,则![]()
由![]()
![]() 又
又![]()
![]()
所以![]()
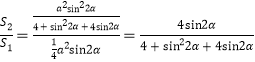
令![]() ,由
,由![]() 得
得![]() ,所以
,所以![]()
![]()
![]()
设![]() ,任取
,任取![]() ,
,
则![]()
![]() 在
在![]() 上单调减,所以
上单调减,所以![]() ,
,
所以![]()
所以![]() 的最大值为
的最大值为![]() ,此时
,此时![]()

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目