题目内容
9.如图,两个边长都为1的正方形并排在一起,则tan(α+β)=3;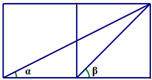
分析 由条件利用三角形中的边角关系,求得tanα 和tanβ的值,再利用两角和的正切公式,求得tan(α+β)的值.
解答 解:由题意可得tanα=$\frac{1}{2}$、tanβ=1,α、β都是锐角,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{\frac{1}{2}+1}{1-\frac{1}{2}×1}$=3,
故答案为:3.
点评 本题主要考查直角三角形中的边角关系,两角和的正切公式,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17.设a=0.23,b=log20.3,c=log0.32,则( )
| A. | b<a<c | B. | b<c<a | C. | c<b<a | D. | a<b<c |
4.在空间直角坐标系O-xyz,点P(1,2,3)关于xOy平面的对称点是( )
| A. | (-1,2,3) | B. | (-1,-2,3) | C. | (1,2,-3) | D. | (1,-2,-3) |
14.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≥0}\\{y≥1}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | -4 | B. | 4 | C. | 2 | D. | 5 |
18.“A,B,C,D四点不在同一平面内”是“A,B,C,D四点中任意三点不在同一直线上”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |


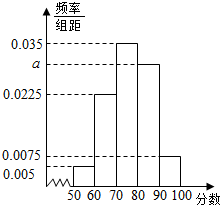 某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.