题目内容
已知等差数列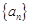 的前
的前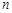 项和为
项和为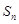 ,且满足:
,且满足: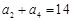 ,
,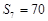 .
.
(1)求数列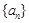 的通项公式;
的通项公式;
(2)设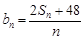 ,数列
,数列 的最小项是第几项,并求出该项的值.
的最小项是第几项,并求出该项的值.
(1)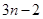 ;(2)4,23
;(2)4,23
解析试题分析:(1)由于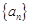 为等差数列,且数列的前
为等差数列,且数列的前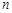 项和为
项和为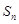 ,且满足:
,且满足: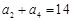 ,
,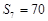 .通过假设首项与公差,根据以上两个条件,列出关于首项、公差的两个等式从而解出首项与公差的值.即可求得等差数列的通项.
.通过假设首项与公差,根据以上两个条件,列出关于首项、公差的两个等式从而解出首项与公差的值.即可求得等差数列的通项.
(2)由(1)可求得等差数列的前n项和的的等式,从而求出数列 的通项公式.根据数列
的通项公式.根据数列 的等式再利用基本不等式可求得结论.
的等式再利用基本不等式可求得结论.
试题解析:(1)设公差为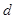 ,则有
,则有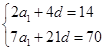 ,即
,即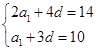
解得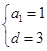 以
以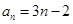
(2)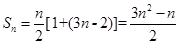
所以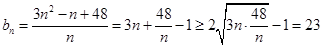
当且仅当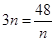 ,即
,即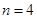 时取等号,
时取等号,
故数列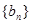 的最小项是第4项,该项的值为23 .
的最小项是第4项,该项的值为23 .
考点:1.等差数列的通项公式,前n项和公式.2.基本不等式的应用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
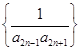 的前n项和.
的前n项和.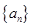 的前
的前 项和为
项和为 ,
,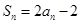 .
. 求数列
求数列 的前
的前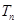 .
.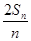 =an+1-
=an+1-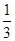 n2-n-
n2-n-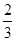 ,n∈N*.
,n∈N*.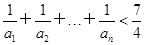 .
.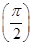 =0.
=0. ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.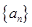 的前
的前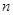 项和为
项和为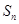 ,满足
,满足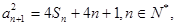 且
且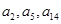 恰好是等比数列
恰好是等比数列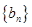 的前三项.
的前三项. ,若对任意的
,若对任意的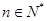 ,
,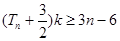 恒成立,求实数
恒成立,求实数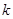 的取值范围.
的取值范围.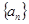 为等差数列,且
为等差数列,且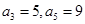 ;数列
;数列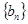 的前n项和为
的前n项和为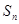 ,且
,且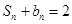 。
。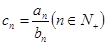 ,
,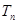 为数列
为数列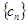 的前n项和,求
的前n项和,求