题目内容
数列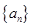 的前
的前 项和为
项和为 ,
,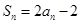 .
.
(1)求数列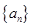 的通项公式;
的通项公式;
(2)设 求数列
求数列 的前
的前 项和
项和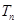 .
.
(1)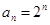 ;(2)
;(2)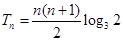 .
.
解析试题分析:(1)先由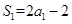 算出
算出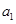 ,当
,当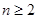 时,由
时,由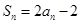 得到
得到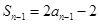 ,两式相减可得
,两式相减可得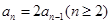 ,从而可判断数列
,从而可判断数列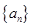 是一个等比数列,再由等比数列的通项公式可写出
是一个等比数列,再由等比数列的通项公式可写出 即可;(2)由(1)中求出的
即可;(2)由(1)中求出的 ,计算出
,计算出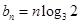 ,这是一个关于
,这是一个关于 的一次函数,故数列
的一次函数,故数列 为等差数列,利用等差数列的前
为等差数列,利用等差数列的前 项和公式求和即可.
项和公式求和即可.
试题解析:(1)当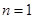 时,
时,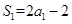 ,∴
,∴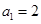 2分
2分
当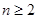 时,
时,
∴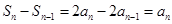
∴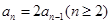 5分
5分
∴数列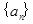 是首项为2,公比为2的等比数列
是首项为2,公比为2的等比数列
∴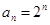 7分
7分
(2)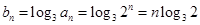 9分
9分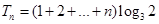 11分
11分
∴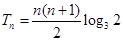 13分.
13分.
考点:1.数列的通项公式;2.等比数列的定义及通项公式;3.等差数列的前 项和公式.
项和公式.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
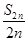 =2013,求n的值;
=2013,求n的值;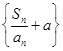 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+ .
.
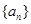 是等差数列,公差为
是等差数列,公差为 ,首项
,首项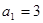 ,前
,前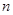 项和为
项和为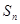 .令
.令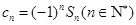 ,
,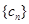 的前
的前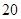 项和
项和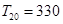 .数列
.数列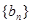 满足
满足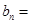
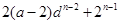 ,
,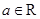 .
.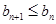 ,
,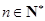 ,求
,求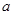 的取值范围.
的取值范围. ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.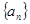 是等差数列,前n项和是
是等差数列,前n项和是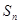 ,且
,且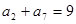 ,
,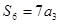 ,
,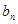 =
=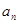 ·2n,求数列
·2n,求数列 的前n项和
的前n项和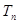
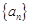 的前
的前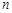 项和为
项和为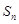 ,且满足:
,且满足: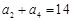 ,
,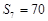 .
.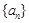 的通项公式;
的通项公式;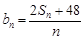 ,数列
,数列 的最小项是第几项,并求出该项的值.
的最小项是第几项,并求出该项的值.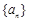 的前
的前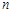 项和为
项和为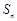 ,已知
,已知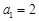 ,
,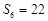 .
.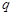 的等比数列
的等比数列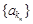 ,其中
,其中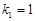 ,且
,且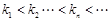 ,
,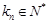 .
.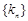 的通项公式;
的通项公式;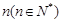 的不等式
的不等式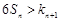 有解,试求
有解,试求