题目内容
22.(本小题满分10分)
已知动圆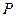 过点
过点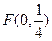 且与直线
且与直线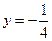 相切.
相切.
(Ⅰ)求点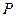 的轨迹
的轨迹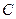 的方程;
的方程;
(Ⅱ)过点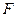 作一条直线交轨迹
作一条直线交轨迹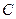 于
于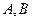 两点,轨迹
两点,轨迹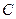 在
在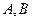 两点处的切线相交于点
两点处的切线相交于点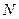 ,
,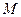 为线段
为线段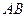 的中点,求证:
的中点,求证: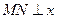 轴.
轴.
已知动圆
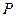 过点
过点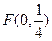 且与直线
且与直线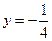 相切.
相切.(Ⅰ)求点
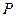 的轨迹
的轨迹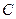 的方程;
的方程;(Ⅱ)过点
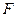 作一条直线交轨迹
作一条直线交轨迹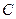 于
于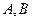 两点,轨迹
两点,轨迹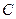 在
在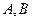 两点处的切线相交于点
两点处的切线相交于点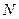 ,
,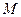 为线段
为线段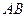 的中点,求证:
的中点,求证: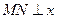 轴.
轴.
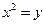
(Ⅰ)根据抛物线的定义,可得动圆圆心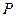 的轨迹C的方程为
的轨迹C的方程为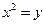 ……………………4分
……………………4分
(Ⅱ)证明:设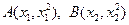 , ∵
, ∵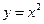 , ∴
, ∴ 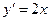 ,∴
,∴ 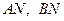 的斜率分别
的斜率分别
为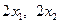 ,故
,故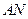 的方程为
的方程为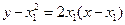 ,
, 的方程为
的方程为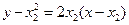 …7分
…7分
即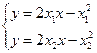 ,两式相减,得
,两式相减,得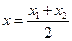 ,
,
∴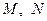 的横坐标相等,于是
的横坐标相等,于是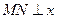 轴……………………………………………………10分
轴……………………………………………………10分
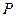 的轨迹C的方程为
的轨迹C的方程为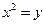 ……………………4分
……………………4分(Ⅱ)证明:设
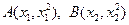 , ∵
, ∵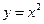 , ∴
, ∴ 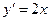 ,∴
,∴ 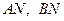 的斜率分别
的斜率分别为
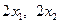 ,故
,故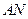 的方程为
的方程为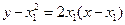 ,
, 的方程为
的方程为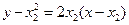 …7分
…7分即
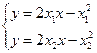 ,两式相减,得
,两式相减,得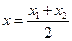 ,
,∴
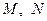 的横坐标相等,于是
的横坐标相等,于是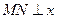 轴……………………………………………………10分
轴……………………………………………………10分
练习册系列答案
相关题目
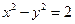 的右焦点为
的右焦点为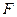 ,过点
,过点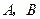 两点,点
两点,点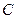 的坐标是
的坐标是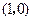 .
.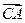 ,
,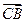 为常数;
为常数; 满足
满足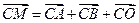 (其中
(其中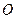 为坐标原点),求点
为坐标原点),求点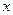 轴距离之和为4的点P轨迹为曲线C,直线
轴距离之和为4的点P轨迹为曲线C,直线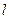 过点F,交曲线C于M,N两点。
过点F,交曲线C于M,N两点。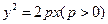 上的一点,弦SC,SD分别交
上的一点,弦SC,SD分别交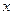 轴于A,B两点,且SA=SB。
轴于A,B两点,且SA=SB。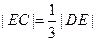 ,求
,求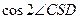 的值。
的值。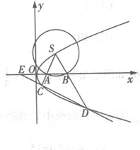
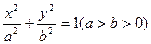 引两条切线,切点分别为B,C,且
引两条切线,切点分别为B,C,且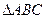 为正三角形.
为正三角形.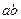 最大时椭圆的方程;
最大时椭圆的方程;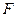 ,过
,过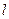 与
与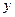 轴交于点
轴交于点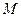 ,与椭圆的一个交点为
,与椭圆的一个交点为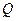 ,且
,且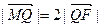 求直线
求直线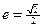 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线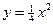 的焦点重合.
的焦点重合.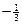 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.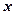 轴,长轴长
轴,长轴长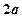 为10,离心率为
为10,离心率为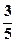 ,则该椭圆的标准方程为 。
,则该椭圆的标准方程为 。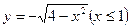 的长度是 .
的长度是 .