题目内容
12.在数列{an}中,a1=1,a4=7,an+2-2an+1+an=0(n∈N﹢)(1)求数列an的通项公式;
(2)若bn=$\frac{1}{n(3+{a}_{n})}$)(n∈N+),求数列{bn}的前n项和Sn.
分析 (1)通过an+2-2an+1+an=0(n∈N﹢)可知数列{an}为等差数列,进而可得结论;
(2)通过an=2n-1,裂项可得bn=$\frac{1}{2}•$($\frac{1}{n}$-$\frac{1}{n+1}$),并项相加即可.
解答 解:(1)∵an+2-2an+1+an=0(n∈N﹢),
∴an+2-an+1=an+1-an(n∈N﹢),
即数列{an}为等差数列,
∵a1=1,a4=7,
∴公差d=$\frac{{a}_{4}-{a}_{1}}{3}$=$\frac{7-1}{3}$=2,
∴an=1+2(n-1)=2n-1;
(2)∵an=2n-1,
∴bn=$\frac{1}{n(3+{a}_{n})}$=$\frac{1}{n(3+2n-1)}$=$\frac{1}{2}$•$\frac{1}{n(n+1)}$=$\frac{1}{2}•$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Sn=$\frac{1}{2}•$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=$\frac{1}{2}•$(1-$\frac{1}{n+1}$).
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知$\overrightarrow{OA}$=$\overrightarrow{i}+3\overrightarrow{k}$,$\overrightarrow{OB}$=$\overrightarrow{j}+3\overrightarrow{k}$,则△OAB的面积为( )
| A. | $\frac{\sqrt{19}}{2}$ | B. | 2$\sqrt{19}$ | C. | $\sqrt{19}$ | D. | 8$\sqrt{19}$ |
7.下列不是古典概型的是( )
| A. | 从6名同学中,选出4名参加数学竞赛,每个人被选中的可能性大小 | |
| B. | 同时掷两枚骰子,点数和为7的概率 | |
| C. | 近三天中有一天降雪的概率 | |
| D. | 10个人站成一排,其中甲,乙相邻的概率 |
1.某程序框图如图所示,该程序运行后输出的S的值是( )
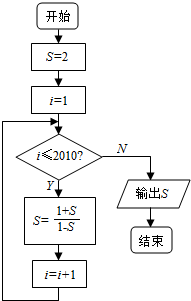

| A. | 2 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
2.设随机变量x~N(1,δ2),若P(x>2)=0.3,则P(x>0)等于( )
| A. | 0.3 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
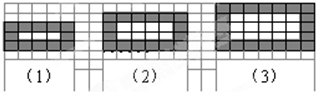 如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.
如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.