题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,当
,当![]() 时,对任意
时,对任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析.
(2)![]() .
.
【解析】分析:(1)先求一阶导函数![]() 的根,求解
的根,求解![]() 或
或![]() 的解集,写出单调区间。
的解集,写出单调区间。
(2)当![]() 时,求出
时,求出![]() 的最小值,存在
的最小值,存在![]() ,使
,使![]() 的最小值,
的最小值,
再分离变量构建函数![]() ,解
,解![]() 。
。
详解:(1)![]() 的定义域为
的定义域为![]() ,
,
又![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
当![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ,
,
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增.
上单调递增.
当![]() ,则
,则![]() ,可得
,可得![]() ,
,
此时函数![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,则
时,则![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ,
,
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增.
上单调递增.
(2)当![]() 时,由(1)得函数
时,由(1)得函数![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 和
和![]() 上单调递增,
上单调递增,
从而![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
对任意![]() ,存在
,存在![]() ,使
,使![]() ,
,
即存在![]() ,
,![]() 函数值不超过
函数值不超过![]() 在区间
在区间![]() 上的最小值
上的最小值![]() .
.
由![]() 得
得![]() ,
,![]() .
.
记![]() ,则当
,则当![]() 时,
时,![]() .
.
![]()
![]() ,当
,当![]() ,显然有
,显然有![]() ,
,
当![]() ,
,![]() ,
,
故![]() 在区间
在区间![]() 上单调递减,得
上单调递减,得![]() ,
,
从而![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某地区某长产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2018(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() (
(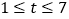 )为何值时,销售额
)为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: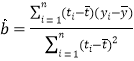 ,
,![]() .
.