题目内容
【题目】设
、
、
表示不同的直线，
、
、
表示不同的平面，给出下列
个命题：其中命题正确的个数是（ ）
①若
，且
，则
；
②若，且
，则
；
③若
，
，
，则
；
④ 若，，，且
，则.
A.
B.
C.
D.
【答案】B
【解析】
①根据两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面，可判断①的正误；
②根据直线与平面平行的判定定理，可判断②的正误；
③根据空间中直线与平面的位置关系，可判断③的正误；
④根据空间中直线与平面平行的性质定理，可判断④的正误.
对于命题①，当
，且
，则
，命题①正确；
对于命题②，当，且
，则
或
，命题②错误；
对于命题③，当
，
，
时，
或
、
、
三条直线交于一点，命题③错误；
对于命题④，
，
，
，，由直线与平面平行的性质定理可得
，同理可得
，由平行关系的传递性可知，命题④正确.
因此，正确的命题为①④.
故选：B.
练习册系列答案
相关题目
【题目】近期，某公交公司与银行开展云闪付乘车支付活动，吸引了众多乘客使用这种支付方式．某线路公交车准备用20天时间开展推广活动，他们组织有关工作人员，对活动的前七天使用云闪付支付的人次数据做了初步处理，设第x天使用云闪付支付的人次为y，得到如图所示的散点图．
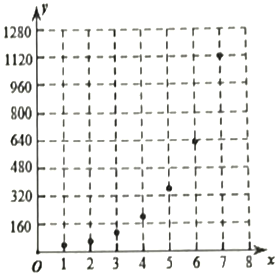
由统计图表可知，可用函数y＝abx拟合y与x的关系
（1）求y关于x的回归方程；
（2）预测推广期内第几天起使用云闪付支付的人次将超过10000人次．
附：①参考数据
|
|
|
|
|
|
4 | 360 | 2.30 | 140 | 14710 | 71.40 |
表中vi＝lgyi，
lgyi
②参考公式：对于一组数据（u1，v1），（u2，v2）…，（un，vn），其回归直线v＝α+βu的斜率和截距的最小二乘估计分别为β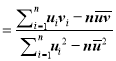
，α
．
