题目内容
((本小题满分13分)
已知a>0,函数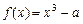 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线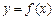 在点M(x1,
在点M(x1,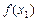 )处的切线为l.
)处的切线为l.
(1)求l的方程;
(2)设l与x轴的交点为(x2,0).证明:
①x2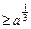 ;②若x1
;②若x1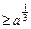 ,则
,则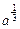 <x2<x1.
<x2<x1.
已知a>0,函数
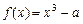 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线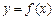 在点M(x1,
在点M(x1,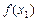 )处的切线为l.
)处的切线为l.(1)求l的方程;
(2)设l与x轴的交点为(x2,0).证明:
①x2
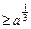 ;②若x1
;②若x1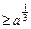 ,则
,则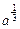 <x2<x1.
<x2<x1. (1)解:求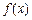 的导数:
的导数: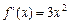 ,由此切线l的方程为
,由此切线l的方程为

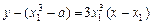 .…………………………………3分
.…………………………………3分
(2)证明:依题意,切线方程中令y=0,
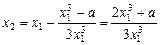 .
.
①x2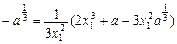
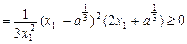
所以x2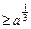 ,当且仅当x1
,当且仅当x1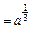 时等号成立.……………8分
时等号成立.……………8分
②若x1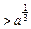 ,则
,则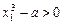 , x2- x1=
, x2- x1=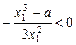 ,
,
且由x2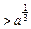 ,所以
,所以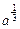 <x2<x1.……………………………13分
<x2<x1.……………………………13分
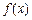 的导数:
的导数: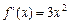 ,由此切线l的方程为
,由此切线l的方程为
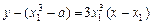 .…………………………………3分
.…………………………………3分(2)证明:依题意,切线方程中令y=0,
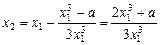 .
.①x2
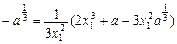
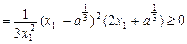
所以x2
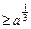 ,当且仅当x1
,当且仅当x1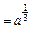 时等号成立.……………8分
时等号成立.……………8分②若x1
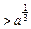 ,则
,则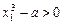 , x2- x1=
, x2- x1=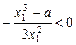 ,
,且由x2
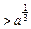 ,所以
,所以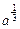 <x2<x1.……………………………13分
<x2<x1.……………………………13分略

练习册系列答案
相关题目
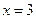 是函数
是函数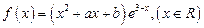 的一个极值点.
的一个极值点.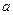 与
与 的关系式(用
的关系式(用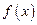 的单调区间;
的单调区间;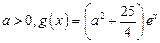 ,若存在
,若存在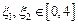 ,使得
,使得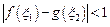 成立,求
成立,求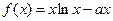 ,
,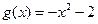 ,
,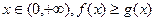 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;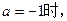 求函数
求函数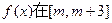 (
(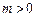 )上的最小值.
)上的最小值.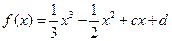 有极值.
有极值.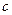 的取值范围;
的取值范围;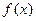 在
在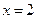 处取得极值,且当
处取得极值,且当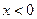 时,
时,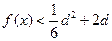 恒成立,求
恒成立,求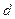 的取值范围.
的取值范围.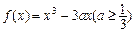 .
.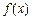 的极小值;
的极小值;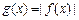 ,x∈[-1,1],求
,x∈[-1,1],求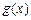 的最大值F(a).
的最大值F(a). )已知函数
)已知函数 ,设
,设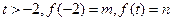 。
。 的取值范围,使得函数
的取值范围,使得函数 在
在 上为单调函数;
上为单调函数;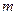 、
、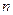 的大小并说明理由;
的大小并说明理由;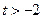 ,总存在
,总存在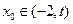 ,满足
,满足 ,并确定这样的
,并确定这样的 的个数。
的个数。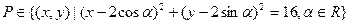 ,则满足条件的点P在
,则满足条件的点P在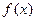 的定义域为
的定义域为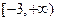 ,且
,且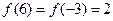 ,
,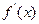 为
为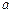 ,
,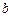 满足
满足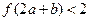 ,则
,则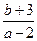 的取值范围是
的取值范围是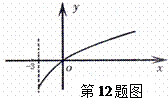
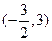
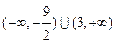
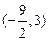
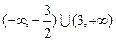
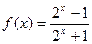 ,(1)判断
,(1)判断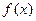 的奇偶性;(2)判断并用定义证明
的奇偶性;(2)判断并用定义证明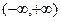 上的单调性
上的单调性